A. Quasi-one-dimensional compressible flow in a variable area duct
| p = rRT | (ideal gas) |
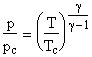 |
(isentropic flow) |
| (energy equation) |
imply that
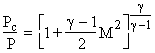
Then from conservation of mass
| (cons. of mass) | |
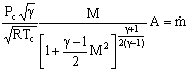 |
The above equation relates the flow area, the mass flow, the Mach number and the stagnation conditions. It is frequently rewritten in a non-dimensional form by dividing through by the value at M=1 (where the area at M=1 is A*):
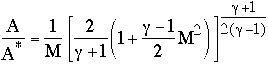
which takes a form something like that shown in Figure 6.1 below
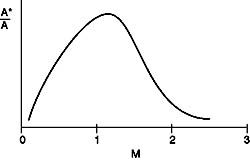
Figure 6.1 General form of relationship between flow area and Mach number.
See this interactively at NASA Glenn - GO! |
B. Thrust in Terms of Nozzle Geometry
We can use these equations to rewrite our expression for rocket thrust in terms of nozzle geometry (throat area = A*, and exit area Ae).
![]()
![]() evaluate at M = 1 (throat)
evaluate at M = 1 (throat)
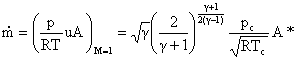
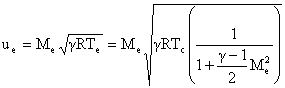
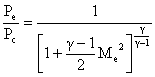
We can now specify geometry (A* and Ae) to determine Me. Then use Me with the combustion chamber conditions to determine thrust and Isp.
Interested in seeing the different types of nozzles out there? - GO! |
| << Previous | Unified Propulsion | Next >> |