5) (20%, partial credit given) When the MIT gas turbine power plant was going through its initial acceptance tests, it experienced a failure. The engine was shut down (fuel flow was turned off). However, the water that is sprayed into the flow in the rear of the combustor (to reduce pollutant emissions) was not shut off. So cold water was sprayed into a very hot, spinning set of turbine blades. The water ended up pooling at the bottom of the circular casing which surrounds the rotating blades causing the casing to cool and then shrink. The casing shrunk to a diameter less than that of the rotating blades, causing the spinning turbine to grind to a halt (and in the process destroyed all the turbine blades--luckily it was still under warranty). [True story]
a) From the point where cold water has pooled at the bottom of the hot casing, until the point where the spinning turbine has come to a screeching halt, describe the energy exchange processes in terms of heat, work and conversion between various forms of energy.
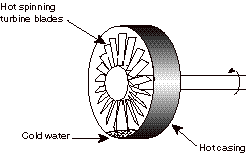
The casing has high internal energy (it is hot). The rotor has high internal energy (it is hot) and high rotational kinetic energy (it is spinning fast). The water has low internal energy (it is cold). Heat is transferred from the hot casing to the cold water. When the internal energy of the casing is lowered, it shrinks, causing it to impinge on the hot spinning rotor blades. The casing does work on the spinning rotor, reducing its kinetic energy. Eventually all of the kinetic energy of the rotor, is converted to internal energy in the casing and the turbine blades/shaft, the water, and the air that surrounds them. (This is analogous to a block sliding along a surface and being decelerated by friction. Eventually all of its kinetic energy ends up as internal energy.)
5 b) If you were asked to estimate how much the average temperature of the casing and turbine changed as a result of the turbine grinding to a halt, how would you make the estimate and what quantities would you need to make the estimate?
First I would neglect the air and the water assuming they are small parts of the problem. [The specific heats for metal, water, and air are all on the same order (within a factor of 10), but the mass of the metal is much greater than the mass of the air or water, so most of the energy will be contained in the metal.]
I would assume that the kinetic energy of the rotating shaft all ends up as internal energy in the casing and turbine. To find the kinetic energy, I need the inertia of the rotating part, I, (mass and geometry information is required) and its rotation rate, w. Then if I know the specific heat of the metal parts, C and I know the combined mass of the rotating part and the stationary part, m, I can determine the change in average temperature of the two parts, DT.
![]()