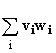 .
.|
|
||
Given two vectors v and w whose components are elements of R, with the same
number of components, we define their dot product, written as
v![]() w or
(v, w) as the sum of the products of corresponding components:
w or
(v, w) as the sum of the products of corresponding components: 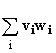 .
.
Obvious facts: the dot product is linear in v and in w and is symmetric between them.
We define the length of v to be the positive square root of (v, v); the length of v is usually denoted by |v|.
Wonderful Fact: the dot product is invariant under rotation of coordinates.
Exercises 3.1 Prove this statement. Solution
As a consequence of this fact, in evaluating v![]() w, we can rotate coordinates so that the first basis vector is in the direction
of v and the second one is perpendicular to it in the plane of v and
w.
w, we can rotate coordinates so that the first basis vector is in the direction
of v and the second one is perpendicular to it in the plane of v and
w.
Then v will have first two coordinates (|v|, 0) and if the angle between
v and w is ![]() ,
w will have (|w|cos
,
w will have (|w|cos![]() ,
|w|sin
,
|w|sin![]() )
as its similarly defined coordinates.
)
as its similarly defined coordinates.
The dot product v![]() w
therefore is |v||w| cos
w
therefore is |v||w| cos![]() ,
in this coordinate system (that is, with these basis vectors), and hence
in any coordinate system obtained by rotations from it.
,
in this coordinate system (that is, with these basis vectors), and hence
in any coordinate system obtained by rotations from it.
The fact that the dot product is linear in each of its arguments is extremely important and valuable. It means that you can apply the distributive law in either argument to express the dot product of a sum or difference as the sum or difference of the dot products.
Exercises 3.2 Express the square of the area of a parallelogram with sides v and w in terms of dot products. Solution
The dot product of v and w divided
by the magnitude of w, which is |v|cos![]() ,
is called the component of v in the direction of w.
,
is called the component of v in the direction of w.
The vector in the w direction having magnitude and sign of |v|cos![]() is called the projection of v on w.
is called the projection of v on w.
The vector obtained by subtracting the projection of v on w from v is called the projection of v perpendicular to w or normal to w. (By definition this projection has zero component in the direction of w, and is therefore normal to w.)
Exercises:
3.3 Express the square of the component of v in the direction of w in terms of dot products. Solution
3.4 Express the component of v perpendicular to w in terms of dot products. Solution
3.5 Write out (v - w)![]() (v
- w) using the linearity of the dot product in each of its arguments. What famous
law does this establish? Solution
(v
- w) using the linearity of the dot product in each of its arguments. What famous
law does this establish? Solution
3.6 Express the projection of v on w in terms of dot products and the vector w. Solution
|
|