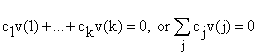 in which some of the c's ar not 0. A set of vectors is said to be linearly
independent if there is no linear dependence among them, and linearly
dependent if there is one or more linear dependence.
in which some of the c's ar not 0. A set of vectors is said to be linearly
independent if there is no linear dependence among them, and linearly
dependent if there is one or more linear dependence.|
|
||
A linear dependency among vectors v(1) to v(k) is an equation, 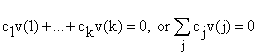 in which some of the c's ar not 0. A set of vectors is said to be linearly
independent if there is no linear dependence among them, and linearly
dependent if there is one or more linear dependence.
in which some of the c's ar not 0. A set of vectors is said to be linearly
independent if there is no linear dependence among them, and linearly
dependent if there is one or more linear dependence.
Example: suppose v(1) = i + j; v(2) =2i; v(3) = 3j.
Then v(1), v(2) and v(3) are linearly dependent because there is the relation
6v(1) = 3v(2) + 2v(3), or 6v(1) - 3v(2) - 2v(3) = 0
Exercise 3.11 Prove: any k + 1 k-vectors are linearly dependent. (You can do it by using mathematical induction.) (If you are not familiar with mathematical induction read this solution and become familiar with it!) Solution
|
|