|
|
||
We define differentiability in two dimensions as follows. A function f of two variables is differentiable at argument (x0, y0) if the surface it defines in (x, y, f) space looks like a plane for arguments near (x0, y0).
(Given any positive numerical criterion, there is a circle around (x0, y0) within which its graph differs from the plane by less than that criterion.)
Recall that a plane in variables f, x and y is defined by a linear equation that can be put in the form
f(x, y) = a (x - x0) + b (y - y0) + f(x0, y0) (A)
The plane that f resembles here is called the tangent plane to f at (x0, y0) and the function it represents is called the linear approximation to f defined at (x0, y0).
The quantities a and b are called the partial derivatives of f with respect to x and with respect to y, and written as follows
![]()
Here a is the directional derivative of f in the direction of the x axis, i, while b is the directional derivative of f in the direction of the y axis, j.
The linear approximation to f(x, y) at arguments x0 and y0 which describes the tangent plane to f at (x0, y0) therefore takes the form
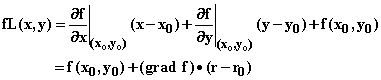
where the vector grad f, called the gradient vector to f at (x0,
y0), is the vector whose components are the partial derivatives
of f in the x and y directions at the point (x0, y0)
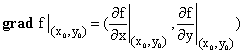
We generally do not write out the cumbersome subscripts that indicate the point (x0, y0) at which the gradient and linear approximation are defined, because they are so cumbersome, and simply write
![]()
Notice that we can write grad f as ![]() with the symbol
with the symbol ![]() ,
called "del" representing the combination
,
called "del" representing the combination![]() .
.
|
|