|
|
||
The second important combination of partial derivatives of a vector field v is its curl.
This is the cross product of the differential operator ![]() with the vector v
with the vector v
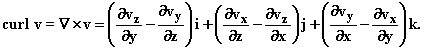
Though again we will defer full explanation of the meaning of this entity we can observe some important properties which give it great importance in themselves.
Since we can create a vector from a scalar by taking its gradient, we can ask:
What happens if we now take the curl of the resulting gradient? That is, what is curl grad f? We can also ask. What is div curl v? And what is div grad f?
The first two of these questions have wonderfully simple answers which are extremely important. The third has an important answer though one whose meaning will not yet be apparent.
Exercises:
9.3 Evaluate div curl v and curl grad f in general; these answers in themselves make curl and div important operators.
9.4 Write down the operator div grad in terms of partial derivatives. (It is often called "the Laplacian". )
|
|