12.3 Spreadsheet Implementation of this Procedure

How can you do such things?
First put x and j in fixed locations X and Y.
Then set up the following columns on the spreadsheet:

f(x_j):

In the first column enter the successive values of f(x_j) starting with the first, known value.

For roots you can start with x₀  = f(x₀) = 1.

Compute later values f(x_j) by using the linear approximation tangent line at x_j-1 evaluated at argument x, fLx_j-1(x) or f(x_j-1) + f '(x_j-1) (x-x_j-1). (x_j-1 is the entry in the second column in the previous row.)

x_j:

In the second column apply the inverse function, f ^-1 to the value in the first column.

Once you have entered your instructions for f(x₁) and x₁, you can copy these down a hundred rows, and you are done.

What happens if f is a root, x^1/m?

In general we have

f(x_j) = fLx_j-1(x) = f(x_j-1) + (x - x_j-1)f '(x_j-1)

 For j-th root,  so that this formula reduces to

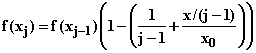
And that is all you need enter. The rest is copying down.