|
Home | 18.013A | Chapter 15 |
||
|
|
||
Computation of curvature and the various directions of interest with respect to the curve is quite straightforward, given a parametric representation of the curve, so that we can instruct a spreadsheet to compute everything here along our curve with a handful of instructions.
The vector ![]() ,
by the chain rule is
,
by the chain rule is ![]() is the reciprocal of
is the reciprocal of![]() and also can be written as
and also can be written as ![]() .
.
Since T is the unit vector in the direction of ![]() .
.
The derivative of this latter expression with respect to t is, by the quotient rule
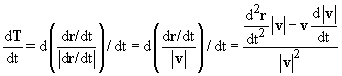
We can identify ![]() with the acceleration of the motion which we denote by a(t).
with the acceleration of the motion which we denote by a(t).
We need here differentiate |v| with respect to t, which,
given that ![]()
Putting all this together we find
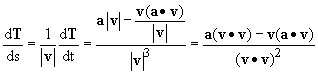
This result looks somewhat messy but it actually not so bad. Recall
that ![]() is
the projection of a normal to v. Therefore we have here that
is
the projection of a normal to v. Therefore we have here that ![]() is the projection of a normal to v divided by the square of
the magnitude of v.
is the projection of a normal to v divided by the square of
the magnitude of v.
Thus the curvature ![]() ,
which is the magnitude of this vector, is the component of a normal to v divided
by the square of the magnitude of v.
,
which is the magnitude of this vector, is the component of a normal to v divided
by the square of the magnitude of v.
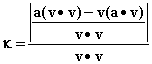
Consider the example of the helix: x = cos t, y = sin t, z = t.
We can compute:![]()
Here a and v are perpendicular, so that we get ![]() for
all values of t.
for
all values of t.
The center of curvature is at the reflection of the point on the
curve at which we compute it, through the z axis, that is, at the point with
coordinates (-cos t, - sin t, t), a distance 2 (or ![]() )
from (cos t, sin t ,t) in the direction of the projection of a normal
to v.
)
from (cos t, sin t ,t) in the direction of the projection of a normal
to v.
Exercises:
15.1 Show that the curvature of a circle is ![]() .
(This proves that the radius of curvature is
.
(This proves that the radius of curvature is ![]() .)
.)
15.2 Find the curvature ![]() ,
position r, and center of curvature at
,
position r, and center of curvature at ![]() for j = 0 to 700 for the following curve (using a spreadsheet)
for j = 0 to 700 for the following curve (using a spreadsheet)
x= cos t, y = cos 2t, z = sin 3 t
Chart it as best you can.
15.3 Set this curve up on the applet. Where is the curvature greatest.
|
|