|
Home | 18.013A | Chapter 26 |
||
|
|
||
Use of the trapezoid rule, which is substantially better than use of the left hand rule for approximating integrals numerically, can be applied here if you can find a way to calculate f(x, y) at the right ends of the intervals when you only have an estimate for y at the left end.
An obvious first approximation to doing this is to approximate y at the right end of the interval using the linear approximation to y defined at the left end. The resulting rule is
![]()
This rule consists of approximating the difference between the values of y at the ends of the interval by half of d multiplied the sum of the derivative f at the left end and the linear approximation to the derivative at the right end defined at the left end. When f does not depend on y we get the usual trapezoid rule.
Another way to look at this for subinterval from x to x + d is by defining "iterations" of the left hand rule, as follows
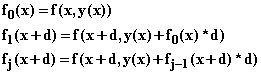
In these terms the computation rule here is
![]()
The left hand rule is off because y changes over the interval. The linear approximation to y applied here is off only because y's derivative changes, and this is a second derivative effect.
Thus the error it causes is quadratic in the interval size, and is on a par with the error intrinsic to the trapezoid rule. We therefore expect this rule to give results that improve in accuracy by a factor of four when N is doubled.
Again, there is no great complication in setting up a spreadsheet to compute the predictions of this rule for any N and you can extrapolate as before with it.
It has the advantage that you can start with the factor 4 extrapolation because accuracy improvement by a factor of 4 on doubling the number of points is built into its structure.
The rule no longer has the same weight structure as the trapezoid rule because when you compute f(x, y) at a given intermediate point from the left you are using the linear approximation at the previous point, while when you compute it in the interval to its right you use the value of y computed from the rule itself in the previous interval. Such is life.
Here are the entries in rows 9 and 10 that can be used in place of those above to produce this computation, when those in red are copied down. The red entries in columns D and E are given for the differential equation y' = x + y. They have to be changed and the results copied down, in order to switch to a different differential equation.
|
B |
C |
D |
E |
|
|
X |
y=y(x-d)+(f0(x-d)+f1(x))*d/2 |
f0(x)=x+y(x) |
f1(x+d)=x+d+y(x)+d*f0(x) |
8 |
|
=B3 |
=B6 |
=B9+C9 |
=B10+C9+(B10-B9)*D9 |
9 |
|
=B9+$B$7 |
=C9+(D9+E9)*(B10-B9)/2 |
=B10+C10 |
=B12+C10+(B12-B10)*D10 |
10 |
Exercise 26.2 Compare the results obtained using the rule above, with those obtained using the left hand rule, upon the same problem.
Here are results obtained using this trapezoid like method with various levels of extrapolation
|
N\L# |
L1 |
L2 |
L3 |
L4 |
L5 |
L6 |
L7 |
L8 |
|
1 |
5 |
|||||||
|
2 |
9.5 |
11 |
||||||
|
4 |
10.9458 |
11.42773 |
11.48883929 |
|||||
|
8 |
11.52449 |
11.71739 |
11.75877194 |
11.77676745 |
||||
|
16 |
11.70817 |
11.76939 |
11.77681781 |
11.77802087 |
11.7780613 |
|||
|
32 |
11.75976 |
11.77696 |
11.77804039 |
11.77812189 |
11.77812515 |
11.77812617 |
||
|
64 |
11.77341 |
11.77796 |
11.77810835 |
11.77811289 |
11.77811259 |
11.7781124 |
11.77811229 |
|
|
128 |
11.77692 |
11.77809 |
11.77811199 |
11.77811223 |
11.77811221 |
11.7781122 |
11.7781122 |
11.7781122 |
The accuracy of these calculations for this problem are shown in the following table
|
N\L# |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
-0.57548 |
|
||||||
|
2 |
-0.19342 |
-0.06606 |
||||||
|
4 |
-0.07067 |
-0.02975 |
-0.02456 |
|
|
|||
|
8 |
-0.02153 |
-0.00516 |
-0.00164 |
-0.00011 |
|
|||
|
16 |
-0.00594 |
-0.00074 |
-0.00011 |
-7.8E-06 |
-4E-06 |
|||
|
32 |
-0.00156 |
-9.8E-05 |
-6.1E-06 |
8.23E-07 |
1.1E-06 |
1.19E-06 |
|
|
|
64 |
-0.0004 |
-1.3E-05 |
-3.3E-07 |
5.84E-08 |
3.4E-08 |
1.68E-08 |
7.6E-09 |
|
|
128 |
-0.0001 |
-1.6E-06 |
-1.8E-08 |
2.51E-09 |
7.1E-10 |
1.84E-10 |
5.3E-11 |
2.4E-11 |
|
Proportional Error for (f0(x) + f1(x+d))/2 Rule y' = y + z, y(0) = 1,finding y(2) |
||||||||
You will note that the estimates here without extrapolation are a little better than those for the first iteration of the previous method, by a factor of 6 for N = 128. However, after extrapolation the results are more accurate by a factor of thousands than in the previous table. See First Order ODE Applet
|
|