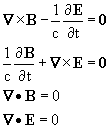
|
Home | 18.013A | Chapter 29 |
||
|
|
||
We now consider what Maxwell's equations tell us about the behavior of electric and magnetic fields in empty space, where there are no charges or currents. Under these circumstances the equations become
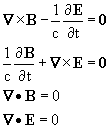
If we take the time derivative of the first and take the curl of the second we find
![]()
We can use the vector identity![]() and the Maxwell equation
and the Maxwell equation ![]() to make this equation into
to make this equation into
![]()
or
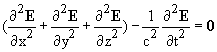
Exercise 29.2 Apply the same manipulations to the same equations taking the curl of the first and the time derivative of the second, to obtain, in the absence of charge or matter
.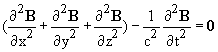
This equation, which both B and E obey in empty space, is called the wave equation. It is a partial differential equation and looks quite formidable, but it is quite easy to find solutions. If you choose any direction in space, and call it the x direction, then any vector function of the variable x - ct, (and any function of x + ct) will obey it.
Exercise 29.3 Verify this claim by differentiating, and using the chain rule.
Solutions of either of these forms "move" with velocity c in space in the forward or backward x directions. They are called plane waves as they are constant over the plane normal to the x direction. Maxwell got the idea that light might consist of such waves. The constant c that occurs in his equations is measurable from electromagnetic experiments, and the velocity of light had recently been measured when Maxwell formulated this notion, and they turned out to be the same within experimental error.
|
|