|
Home | 18.013A | Chapter 33 |
||
|
|
||
We will consider equations in which there are one or more dependent variables, and a single independent variable, and we have expressions for the second derivative of the dependent variables.
Some examples are:
The forced damped harmonic oscillator
![]()
A circuit equation
![]()
Planetary motion
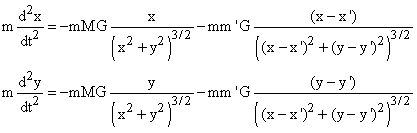
(The second terms are the effects of another planet whose position will obey similar equations.)
The pendulum
![]()
The first two of these are linear equations in that each term is linear in the dependent variable or independent of it.
Physicists tend attack equations of this kind (when they can) by finding combinations of the variables and first derivatives that have vanishing time derivative. These are called integrals or constants of the motion. Energy, angular momentum and momentum are among the entities that are often conserved. The constancy of such quantities provides equations that can then be used to help determine the motion.
There are all sorts of methods that have been deployed to solve linear differential equations, including power series expansions, and "transformations" on function spaces.
We confine ourselves here to indicating how to solve differential equations on a spreadsheet. There is a whole course devoted to their study.
|
|