1.2 Numbers

]> 1.2 Numbers

Home \| 18.013A \| Chapter 1		Tools Glossary Index Up Previous Next

1.2 Numbers

We start with the basic concept of a number. The Natural Numbers, denoted as $ℕ$ , are the numbers 1,2,3,... These are closed under Addition.

A set that can be put in correspondence with $ℕ$ or a subset of $ℕ$ is called countable.

Introducing the notion of subtraction makes us enlarge $ℕ$ to get the Integers, denoted as $ℤ$ , positive or negative or 0, so that our numbers are closed under the operation of substraction.

Exercise 1.1 Is $ℤ$ countable? Solution

$ℤ$ is closed under multiplication; which is to say that the product of two integers is an integer.

To obtain a set of numbers closed under Division: we must enlarge $ℤ$ to get the Rational Numbers $ℚ$ , which are fractions of the form $\frac{a}{b}$ where $a$ is in $ℤ$ and $b$ is in $ℕ$ .

Exercises:

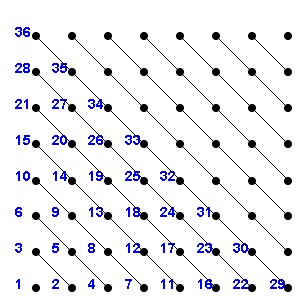
1.2 Is $ℚ$ countable? (See picture for hint.) Solution

1.3 Prove or disprove: a countable set of countable sets is countable. Solution

Decimal form of numbers

The numbers between 0 and 1 can each be represented as a decimal point followed by an infinite string of digits, each digit being one of 1, 2, 3, ..., 9, 0.

Rational numbers repeat themselves endlessly after some point: (for example 1 / 4 is .250* or also .249* where the star means that you repeat the starred digit endlessly) 1 / 3 is .3*, 1 / 7 = .(142857)*, 57 / 100 = .570*.

Irrational numbers do not do so.

Exercises:

1.4 Prove that rational numbers repeat the same finite sequence of digits endlessly, and that irrational numbers do not. Solution

1.5 Are there non-rational decimal digit sequences? Solution

1.6 Are all such sequences countable? (See picture for hint.) Solution

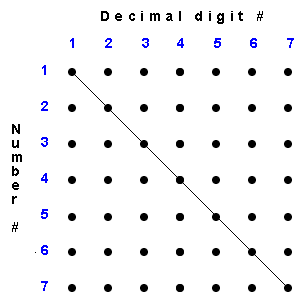
A number which differs from the number in the k-th position on the list in its k-th decimal digit, cannot be in any position on the list of numbers!

Algebraic numbers are solutions to polynomial equations, with integer coefficients.

Exercise 1.7 Are algebraic numbers countable? Solution

The Real Numbers $ℝ$ are all distinct infinite sequences of digits, having a sign and a finite number of digits in front of the decimal point.

You can add subtract multiply and divide them except dividing by 0 is not allowed.

Are there other sets that we might dignify by calling numbers?

Yes! There are "Numbers mod $x$ ". These are remainders of $ℤ$ or $ℚ$ or $ℝ$ obtained when you divide by $x$ .

There are also complex numbers, which form the set $ℂ$ . These are expressions of the form $a + i b$ where $i^{2} = - 1$ , $a$ and $b$ are in $ℝ$ , and multiplication and division are as in $ℝ$ with the additional rule above.

Comment - More on Complex Numbers