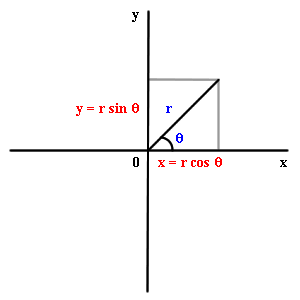
|
|
||
A 2-vector
can be described by two numbers that are not coefficients
in a sum: its length, and the angle its vector makes with the
axis.
The first of these is usually written as
, the second as
.
These parameters obey
and
;
the inverse relations are
.
and
are called polar coordinates.
Calculating the angle in polar coordinates is a bit tricky; the obvious thing to try is but that is defined only between and , while has a domain of size .
Here is something that works: .
This gives theta in the range to . If you want it to have range 0 to you can add to it.
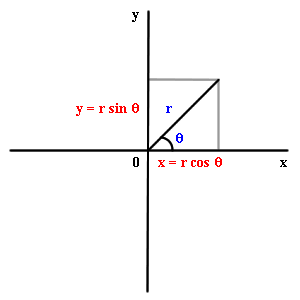
|
|