6.3 Examples of non Differentiable Behavior

A function which jumps is not differentiable at the jump nor is one which has a cusp, like has at .

Generally the most common forms of non-differentiable behavior involve a function going to infinity at , or having a jump or cusp at .

There are however stranger things. The function , for example is singular at even though it always lies between -1 and 1. Its hard to say what it does right near 0 but it sure doesn't look like a straight line.

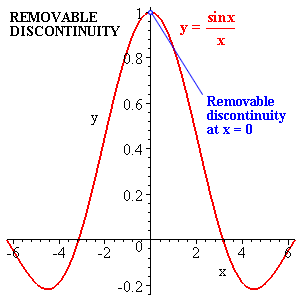
If the function has the form will usually be singular at argument if vanishes there, . However if vanishes at as well, then will usually be well behaved near , though strictly speaking it is undefined there.

We usually define at under such circumstances to be the ratio of the linear approximation at to g to that to very near , which means we define to be , when, of course the denominator here does not vanish. (If the denominator does vanish and the numerator vanishes as well, you can try to define similarly as the ratio of the derivatives of these derivatives, etc.)

This kind of thing, an isolated point at which a function is not defined, is called a "removable singularity" and the procedure for removing it just discussed is called "l' Hospital's rule" .

An example is at .

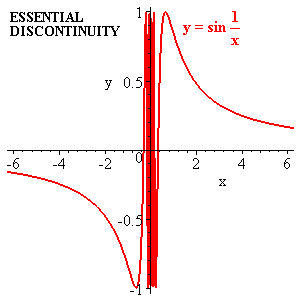
Continuous but non differentiable functions
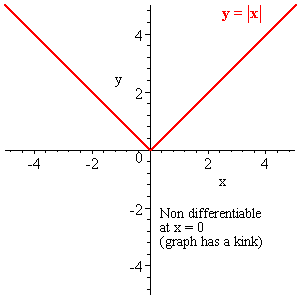
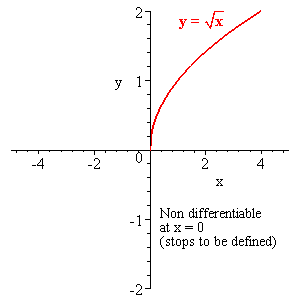
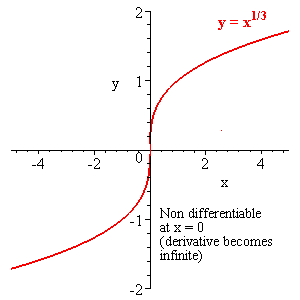