9.4 The Gradient in Polar Coordinates and other Orthogonal Coordinate Systems

Suppose we have a function given to us as

f (x, y)

in two dimensions or as

g (x, y, z)

in three dimensions. We can take the partial derivatives with respect to the given variables and arrange them into a vector function of the variables called the gradient of

f

, namely

(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}) or (\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}, \frac{\partial g}{\partial z})

\frac{\partial f}{\partial x} \hat{i} + \frac{\partial f}{\partial y} \hat{j} or \frac{\partial g}{\partial x} \hat{i} + \frac{\partial g}{\partial y} \hat{j} + \frac{\partial g}{\partial z} \hat{k}

Suppose however, we are given

f

as a function of

r

and

θ

, that is, in polar coordinates, (or

g

in spherical coordinates, as a function of

φ, θ

, and

ρ

For example, suppose

f = \frac{1}{r}

, or

g = \frac{1}{ρ}

, or

g = \sin θ

One way to find the gradient of such a function is to convert $r$ or $ρ$ or $θ$ into rectangular coordinates using the appropriate formulae for them, and perform the partial differentiation on the resulting expressions.

\frac{1}{r} = {(x^{2} + y^{2})}^{- 1 / 2}

\overset{⟶}{\nabla} \frac{1}{r} = - \frac{x}{r^{3}} \hat{i} - \frac{y}{r^{3}} \hat{j}

It is a bit more convenient sometimes, to be able to express the gradient directly in polar coordinates or spherical coordinates, like it is expressed in rectangular coordinates as above.

We want here an expression involving partial derivatives with respect to

r

and

θ

multiplied by vectors pointing respectively in the $r$ direction, and $θ$ direction.

So we want to know: what vectors should these partial derivatives be multiplied by in order to form the gradient?

When we find the answer, the actual partial derivative with respect to each polar variable will be the dot product of a unit vector in a polar direction with the gradient.

We therefore digress to discuss what thes unit vectors are so that you can recognize them.

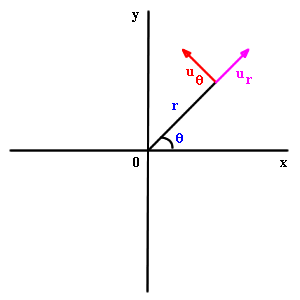
The r direction is the direction tilted by an angle

θ

counterclockwise from the

x

axis. A unit vector in that direction, call it

\overset{⟶}{u_{r}}

, can be written in any of the three following forms

\overset{⟶}{u_{r}} = \cos θ \hat{i} + \sin θ \hat{j} = \frac{x}{r} \hat{i} + \frac{y}{r} \hat{j} = \frac{\overset{⟶}{r}}{r}

The unit vector in the

θ

direction lies in the direction

90 °

beyond the

r

direction, counterclockwisely, and is therefore given by

\overset{⟶}{u_{θ}} = - \sin θ \hat{i} + \cos θ \hat{j} = - \frac{y}{r} \hat{i} + \frac{x}{r} \hat{j}

We know that if we make differential changes in

r

and

θ

the resulting change in

f

will be given by

d f (r, θ) = \frac{\partial f}{\partial r} d r + \frac{\partial f}{\partial θ} d θ

d f = {(\overset{⟶}{\nabla} f)}_{r} d s_{r} + {(\overset{⟶}{\nabla} f)}_{θ} d s_{θ} = \overset{⟶}{\nabla} f \cdot d s

As we noted briefly in section 3.8 , distance in polar coordinates upon making small changes in the variables

r

and

θ

is described by

d s^{2} = d r^{2} + r^{2} d θ^{2}

{(\overset{⟶}{\nabla} f)}_{r}

is the partial derivative of

f

with respect to

r

, just as

{(\overset{⟶}{\nabla} f)}_{x}

is its partial derivative with respect to

x

But because $d s_{θ}$ has a factor of $r$ in it, there must be a compensating factor of $r$ in the denominator of the component of $\overset{⟶}{\nabla} f$ in the $θ$ direction

{(\overset{⟶}{\nabla} f)}_{θ} = \frac{\partial f}{r \partial θ}

\overset{⟶}{\nabla} f = \frac{\partial f}{r \partial θ} \overset{⟶}{u_{θ}} + \frac{\partial f}{\partial r} \overset{⟶}{u_{r}}

A similar computation can be made for any orthogonal directions in any dimension, and we can anticipate the result.

The component of $\overset{⟶}{\nabla} f$ in the direction of any such variable will be the partial derivative of $f$ with respect to that variable, divided by the ratio of distance change in that direction to change in the variable itself.

Using the last equation we can immediately deduce that the gradient of $θ$ is $\frac{\overset{⟶}{u_{θ}}}{r}$ , except of course at $r = 0$ , where $θ$ is not differentiable. Similarly we find that the gradient of

\frac{1}{r}

- \frac{1}{r^{2}} \overset{⟶}{u_{r}}

9.5 Use the fact that both angular variables in spherical coordinates are polar variables to express $d s^{2}$ in 3 dimensions in terms of differentials of the three variables of spherical coordinates. From this deduce the formula for gradient in spherical coordinates.

9.6 Find the gradient of $ϕ$ in spherical coordinates by this method and the gradient of $θ$ in spherical coordinates also.

There is a third way to find the gradient in terms of given coordinates, and that is by using the chain rule.

We can first consider differential change of

f

in rectangular coordinates, and then relate the differential changes in

x

and

y

to differential changes in the other coordinates, say

r

and

θ

. Combining these we can relate the change in

f

to changes in the latter two variables.

Since we know how to write the gradient in rectangular coordinates and can recognize unit vectors, we can express the resulting expression in terms of components of the gradient in the other coordinate system.

\begin{array}{l} d f = \frac{\partial f}{\partial x} d x + \frac{\partial f}{\partial y} d y \\ d x = \frac{\partial x}{\partial r} d r + \frac{\partial x}{\partial θ} d θ \\ d y = \frac{\partial y}{\partial r} d r + \frac{\partial y}{\partial θ} d θ \end{array}

and use the latter two equations to get rid of

d x

and

d y

in the first equation. The result is an expression for

d f

in terms of

d r

and

d θ

, the coefficients of which can be described in terms of unit vectors in the various directions, and the gradient in rectangular coordinates.

Comparing that equation with the basic formula defining partial derivatives, Equation (A) above you can read off the components of the gradient.

This approach is useful when

f

is given in rectangular coordinates but you want to write the gradient in your coordinate system, or if you are unsure of the relation between

d s^{2}

and distance in that coordinate system.

It is worth noting that when we take the partial derivative with respect to $x$ or $y$ we always mean that we are keeping the other variable, $y$ or $x$ , constant; on the other hand the partials with respect to $r$ and $θ$ always mean keeping the other one of these, $θ$ or $r$ , constant. Any other meaning has to be described explicitly.

There are times and places where in a partial derivative one can become confused as to which variable or variables are being kept constant, and under such circumstances it is wise to modify the notation to supply this information explicitly. Thus we can write

{(\frac{\partial f}{\partial x})}_{y}

to mean the partial derivative with respect to

x

keeping

y

fixed, and then there can be no confusion as to what is kept constant.

You can use it to determine the directional derivative of the function involved, in any direction.

In rectangular coordinates its components are the respective partial derivatives.

The gradient of the sum of two fields is the sum of their gradients (the gradient is a linear operator).

The gradient of a product can be computed by applying the usual product rule for differentiation.

Home \| 18.013A \| Chapter 9		Tools Glossary Index Up Previous Next