» Required Reading » Table of Contents » Chapter 1 1.2 Numbers
	Previous Section	Next Section

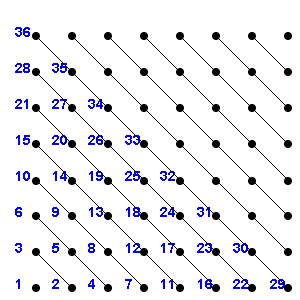
Natural numbers N 1,2,3,…These are closed under Addition.
A set that can be put in correspondence with N or a subset of N is called countable.
Subtraction; makes us enlarge N to get  the Integers Z, positive or negative or 0.

Exercise 1.1  Is Z countable? Solution

Multiplication
To be closed under Division: we must enlarge Z to get the Rational Numbers Q, which are fractions, of the form Z / N.

Exercises:

1.2 Is Q countable? (see picture for hint) Solution

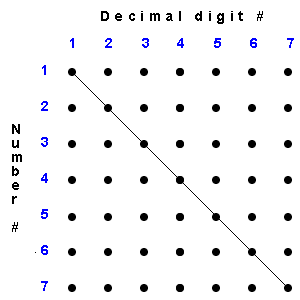
1.3 Prove or disprove: a countable set of countable sets is countable. Solution

Decimal form of numbers
All rational numbers repeat the same sequence of decimal digits forever.
Why?

Exercises:

1.4 Are there other decimal numbers? Solution

1.5 Are all decimal numbers countable? (see picture for hint) Solution

A number which differs from each number k in the kth decimal digit # cannot be on the list of numbers!

Algebraic numbers: these are solutions to polynomial equations, with integer coefficients.

Exercise 1.6 Are algebraic numbers countable? Solution

Real Numbers R = all decimal numbers,
You can add subtract multiply and divide them except dividing by 0 is not allowed.

Other numbers?
Numbers mod x are remainders on dividing by x.
Complex numbers C are numbers of the form aib where i² = -1 and multiplication and division are so defined, and a and b are in R.

Comment