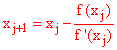» Required Reading » Table of Contents » Chapter 13 13.1 Newton's Method
	Previous Section	Next Section

This method, as just noted, consists of iterating the process of setting the linear approximation of f to 0 to improve guesses at the solution to f = 0.

The linear approximation to f(x) at argument x₀ which we will call f_l (x, x₀) can be described by the equation

if we set fl(x, x₀) = 0, and solve for x, we obtain

and so we obtain , and in general can define

In  the old days the tedium of performing the steps of finding the x_j’s was so formidable that it could not be safely inflicted on students.

Now, with a spreadsheet, we can set this up and do it with even a messy function f, in approximately a minute.
To do so put your initial guess, x₀ in one box say a2, put "= f(a2)" in b2, and "= f '(a2)" in c2. Then put "= a2-b2/c2" in a3 and copy a3, b2 and c2 down as far as you like. That’s all there is to it. If column b goes to zero, the entries in column a will have converged to an answer.

If you want to change your initial guess you need only enter something else in a2; to solve a different equation you need only change b2 and c2 and copy them down. This raises some interesting questions; namely, can we say anything about when this method will work and when it will not?

First you should realize that many functions have more than one argument for which their values are 0. Thus you may not get the solution you want. Also, if the function f has no zero, like x² + 1, you will never get anywhere. Here is another problem: if your initial guess, x₀ (or any subsequent x_j) is near a critical point of f (at which f ' = 0) the quantity -f / f 'may become huge at that argument, and you may be led to looking at arguments very far from what you are looking for. And if f is implicitly defined you may find that some new guess x_j in which f is not even defined, and the iteration will dead end.

Can we say anything positive about the use of the method?
Yes! If f goes from negative to positive at the true solution x, and f ' is increasing between x and your guess x₀, which is greater than x, then the method will always converge. Similar statements hold when f goes from positive to negative, and under many other circumstances.

Why is this? If f ' is increasing, then the tangent line to f at x₀  will go under the f curve at between x and x₀, so that the linear approximation, whose curve it is, will hit zero between x and x₀, and the same thing will be true in each iteration. Thus the x’s will march off toward the true solution without hope of escape and will eventually get there.
Another virtue of the method is that as one gets closer to the solution, the differentiable function will tend to look more and more like its linear approximation between the current guess and the true solution. Thus the method tends to converge very rapidly once that current guess is near a solution.

Exercises:

Set up a spread sheet to apply it to the following functions:

13.1      exp(x) - 27

13.2      sin (x) - 0.1

13.3      x²

13.4      tan x

13.5      x^1/3

13.6      x^1/3 - 1