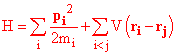» Required Reading » Table of Contents » Chapter 16 16.3 The Hamiltonian
	Previous Section	Next Section

Newton’s laws involve forces, and forces are vectors which are a bit messier to handle and to think about than ordinary functions are. In the Eighteenth and early Nineteenth Centuries physicists got the idea of reformulating the laws of motion in terms of energy functions particularly for systems of interacting objects for which energy is conserved.
The most important such reformulation involves defining a function  called the Hamiltonian of the system. It is the energy E that we have encountered above, but expressed not in terms of position and velocity variables but rather in terms of position and momentum variables.

For example, suppose we have a set of objects each with three position variables and corresponding momentum variables. The momentum variable p_xi corresponding to x_i which itself is the x coordinate of the ith object, is m_iv_xi . The kinetic energy of the object i is then . If there is a potential energy of interaction between them (such as that produced by gravitational attraction, there will be a potential energy term of the form between each pair of objects, i and j. The Hamiltonian, H,  of the system will then look like

The equations of motion, which correspond to F = ma in this formulation are:
For each p_i and r_i, and each direction d we have

(The subscript d here refers to directions x, y and z.), These equations are called Hamilton’s equations.

In actuality they have the same content as Newton’s equations in this context. Their importance lies particularly in that quantum mechanics can be described most easily in terms of the Hamiltonian.

If we choose a function Z of the position and momentum variables here its time dependence can be computed by the chain rule as

Substituting Hamilton’s equations here we get

The somewhat ugly last two terms here are called “the Poisson Bracket” of Z and H, and written as {Z, H}, so that we have

Exercises:

16.1  Consider the system consisting of the sun and the earth, with a potential energy between them of  . Write down Hamilton’s equations for this system.

16.2 A force in the radial direction (plus or minus) is called a central force. The force on the earth implied by the example above is an example of one, if we choose the position of the sun as origin. Compute the time derivative of r_ev_e  in this system for this (or any) central force.