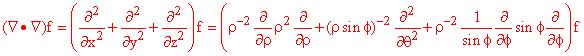» Required Reading » Table of Contents » Chapter 17 17.3 The Divergence in Spherical Coordinates
	Previous Section	Next Section

The previous result is extremely useful in differentiating vectors given in non-rectangular coordinate systems like spherical coordinates. It can be used whenever we can factor v into a relatively simple vector part and a multiplicative factor.
For example, suppose we want to find the divergence of
We can write this as the vector (x, y, z).
On applying this rule, we get

Now we also have

and

so putting this all together we find

There are two other facts that along with this one allow us to express the divergence in spherical coordinates. They are

and

The easiest way to see the first is in rectangular coordinates in which the unit vector in the Since the x derivative of the divergence of this unit vector is 0.
The quantity in parentheses in the second of these equations is the vector

Exercises:

17.1 Verify that the divergence of is 0. (Remember )
We can apply these facts by using the product rule above on each term to obtain the divergence of v.

On applying the product rule to each term and our three facts we get

since the second terms from the product rule all are 0 as follows from these facts.
Recall that in spherical coordinates we have

Applying this equation to each of the terms above we get

This formula appears rather ugly, but it is quite important in physical applications, It appears in particular in the combination which is called the Laplacian of f. In rectangular coordinates and spherical coordinates the Laplacian takes the following forms, which follow from the expressions above for the gradient and divergence.

17.2 Find the divergence of rr^-2 and of zz^-1.

17.3 Deduce from these facts the form of the divergence in cylindric coordinates using the logic used above in spherical coordinates.