|
1. Given the following five vectors:A = (1, 2, 3); B = (2,
-3, 5); C = (x, y, z); D = (cos t, sin t, t2); E = (-2, 1, 0)
Do each of the following:
a) Form the sum: A + B + C.
b) Compute A B. B.
c) Compute A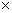 (B+C). (B+C).
d) Find values for x y and z for which C A
= 0 and C A
= 0 and C B
= 0. B
= 0.
e) Find the cosine of the angle between A and B. Between B and D (the answer will
be a function of t).
f) Find the projection of E on B.
g) Find the determinant whose columns are A B and E; also find the determinant
whose columns are A B and C.
h) Suppose the point p has coordinates x = 1, y = 2, z = 3. What are its spherical
coordinates 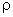 , ,
 and and
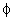 ? ?
i) What is the volume of the parallelepiped with edges A B and E?
j) Find the projection of D into the (x, y) plane. What is its length?
2. Consider the line containing the points A and B above.
a) Give a parametric representation of the points on that line.
b) Find a unit length "tangent vector" that points in the direction
of the line.
c) Find two directions normal to that vector.
d) e) and f) consider the plane containing the points A B and E:
Find a (two parameter) parametric representation of the plane.
Find a normal to the plane.
Find an equation that points on the plane all obey.
g) Suppose we have a new and different product of Vectors V@W that has the property
V@V = 0 for all Vand @ is linear in each argument so that you can apply the distributive
law.
Deduce something about V@W + W@V by applying same to (V + W)@(V + W).
3. Differentiate the following functions with respect to the indicated variables:
a) sin (2exp(x)).
b) (exp (x+y))*sin (xy) with respect to x for fixed y.
c) x2 + y2-3xy with respect to y for fixed x.
d) (sin (y + s (sin t))*(exp -(x+s(cos t))) with respect to s everything else
fixed.
e) Find the gradient of (sin y)exp(-x).
f) Find the directional derivative of this function in the direction whose unit
vector is (cos t, sin t).
g) Find the linear approximation to sin (exp(x)) at x = 0.
h) Evaluate the derivative with respect to t of (r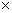 v)
where v is v)
where v is  ;
suppose that ;
suppose that  is in the direction of r. What then is the answer?
is in the direction of r. What then is the answer?
i) Where is  not differentiable? Where is tan x not differentiable? Where is
not differentiable? Where is tan x not differentiable? Where is  not differentiable?
not differentiable?
j) Find the derivative of an inverse function to sin (exp(x)) (to define an inverse
function completely you have to specify a range; ignore that here).
4.
a)Find the gradient of the function 
b) Find the gradient of 
c) Find the gradients of cos  and
of and
of  . .
d) Find the curl of (y, z, x).
e) Find the divergence of 
f) Find the curl of same.
5.
a)Find the quadratic approximation to sin xy at x = 1 y = 2 (radians).
b) Where does this function have critical points (both partial derivatives are
0).
c) Find at least one saddle point.
d) Evaluate (a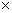 b) b) (a (a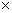 b)
by switching a dot and cross product and expressing the triple cross product according
the rule for doing same, to get an alternate expression for the same thing entirely
in terms of dot products. b)
by switching a dot and cross product and expressing the triple cross product according
the rule for doing same, to get an alternate expression for the same thing entirely
in terms of dot products.
e) Which of the following functions can be defined at x = 0?

|
