2.25 Problem Sets - Section 5

Problem 5.11: Air Cushion Vehicle

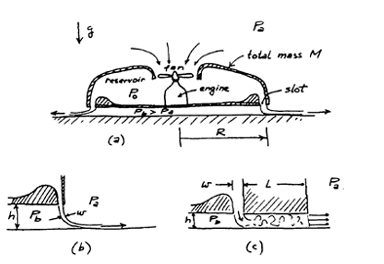
The sketch (a) shows the cross-section of an air cushion vehicle of the "peripheral jet" type, first developed by Christopher Cockerell in the mid-1950s. A fan draws air from the ambient atmosphere at pressure p_a and compresses it to a stagnation pressure p_o in the reservoir inside the vehicle. The air then exhausts downward through a narrow slot of width w at the periphery of the vehicle (w<<R), creating a condition that maintains a positive gage pressure (an "air cushion") underneath the vehicle. This allows the vehicle to float at a height h above the ground.

This problem is concerned with the mechanics of how the "air cushion" is maintained the vehicle holds itself off the ground. In what follows we assume that the vehicle has total mass M and is circular with outer radius R, the slot has a width w that is very small compared with R, the jet issues vertically downward from the slot as shown, and the vehicle's elevation h is always small compared with R. A fan or turbine maintains the pressure in the reservoir at pressure D p₀ = p _a + D p.

In what follows, we proceed with the assumption that the flow from the reservoir to the slot is steady, incompressible and inviscid. To simplify matters, we shall also assume (tentatively) that the pressure p_b under the vehicle is just slightly greater than p_a, such that

p_b - p ₀ << D p.

and justify this à posteriori by showing that our solution is consistent with is assumption.

Given: r, M, g, R, w, D p, where w<<R, h<<R

		General Case: (a) Derive an expression for the outflow velocity V_j in the slot jet.

(b) Show, using the vertical component of the linear momentum theorem, that in steady state operation,

where p_b is the pressure under the vehicle. (The proof of this relation is not quite the self-evident "one-liner" that one might jump to, for when the fan is on, the air drawn toward the inlet on top has velocity and the pressure on the top of the craft is below atmospheric.)

		CASE 1 (Fig. B) Consider first the design (or operating) condition shown in Fig. 2 that is characterized by h >> w. Assume that the jet issues from the slot as a thin, coherent sheet of constant width w which bends around in a circular path until it becomes parallel to the ground, as shown in the figure, after which it follows the ground outward. (This is a bit of a stretch, but it will do as a working approximation.) (c) Use the momentum theorem to obtain an expression for the supporting gage pressure p_b – p_a for Case 1, expressed in terms of the given quantities and h.

(d) Show that the assumption (1) is satisfied in Case 1 because h>>w.

		(e) Obtain an expression for the vehicle's ground clearance h for Case 1 in terms of the given quantities.

(f) The power delivered by the fan to the fluid is given by

W = D pQ

where Q is the volume flow through the device. Express h in terms of W , r, M, g, R, andD p. Show that for given hovercraft size R and ground clearance h, choosing a fan that delivers the requisite power at the lowest pressure D p minimizes the power expenditure per unit system weight, W/M_g . (Note, however, that this does not necessarily mean that power per unit payload weight is minimized. Fans that operate at low pressure are typically larger and heavier than higher-pressure fans with the same power output, and supporting their extra weight consumes some of the power. This must be factored into a true system optimization.)

		CASE 2 (Fig. C) Next consider a design where the slot is set back some distance L from the vehicle’s periphery, as shown in Fig. 3, with L being small compared with R (L << R) but large compared with h (L>>h). In this case, viscous forces cause the jet to become turbulent and spread so it fills the gap under the vehicle's edge by the time the air exits at the periphery. (g) Repeat C-F for Case 2, replacing part D with the following: “Show that assumption (1) is satisfied in Case 2 provided h>>w.” Compare Case 2 with Case 1 and comment. Which design is better?