2.25 Problem Sets - Section 5

Problem 5.8: Jet Pump

Previous Problem | Next Problem

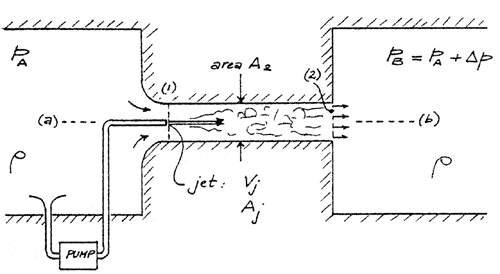
The device connected between compartments A and B is a simplified version of a jet pump. A jet (or ejector) pump is a device which uses a small, very high-speed jet with relatively low volume flow rate to move fluid at much larger volume flow rates against a pressure differential D p, as shown in the figure.

The pump in the figure consists of a contoured inlet section leading to a pipe segment of constant area A₂. A small jet draws fluid from compartment A and ejects it at high velocity V_j and area A_j at the entrance plane (1) of the constant-area pipe segment. Between (1) and (2), the jet (the "primary" stream) and the secondary fluid flow which is drawn in from compartment A via the contoured inlet section mix in a viscous, turbulent fashion and eventually, at station (2), emerge as an essentially uniform-velocity stream. The pump operates in steady state.

To simplify the analysis, we make several physical assumptions that are not unreasonable. We assume

• that the flow is incompressible
• that the flow from compartment A to station (1) is inviscid,
• that, although viscous forces cause the turbulent mixing process between (1) and (2), the shear force exerted on the walls between those stations is small compared with DpA₂,
• that gravitational effects are negligible, the flow being horizontal.

We also make two assumption about operating conditions that are also reasonable and considerably simplify the mathematics involved in the analysis:

A_j << A₂     and      V_jA_j << V₂A₂

(a) Derive an expression for Dp as a function of the total volume flow rate Q from compartment A to compartment B. The given quantities are A₁, A₂, r and V_j. Indicate the volume flow rate Q_o when Dp = 0 (the "short-circuit" volume flow rate) and the pressure Dp₀ at which Q = 0. Write the pressure-volume flow rate relationship in universal dimensionless form as Dp/Dp₀ vs Q/Q₀ and sketch it for positive values of pressure This is the “pump curve” in dimensionless form.

Show that for A_j << A₂, Q₀ >> V_jA_j.

		(b) Sketch the pressure distributions along the line a-b for the cases Dp = 0 and Dp > 0.

		(c) Is your formulation in (a) valid when Q=0, i.e. when the total volume flow rate from A to B is zero? Explain. What is the minimum value Qmin of Q for which your formulation in (a) is valid?