Course Description
This course is an introduction to linear optimization and its extensions emphasizing the underlying mathematical structures, geometrical ideas, algorithms and solutions of practical problems. The topics covered include: formulations, the geometry of linear optimization, duality theory, the simplex method, sensitivity …
This course is an introduction to linear optimization and its extensions emphasizing the underlying mathematical structures, geometrical ideas, algorithms and solutions of practical problems. The topics covered include: formulations, the geometry of linear optimization, duality theory, the simplex method, sensitivity analysis, robust optimization, large scale optimization network flows, solving problems with an exponential number of constraints and the ellipsoid method, interior point methods, semidefinite optimization, solving real world problems problems with computer software, discrete optimization formulations and algorithms.
Course Info
Learning Resource Types
assignment
Problem Sets
notes
Lecture Notes
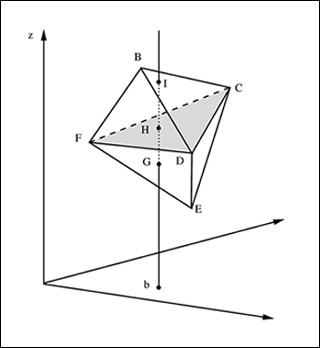
Topics in geometric programming are covered in lectures 2-4. (Courtesy of D. Bertsimas and J. N. Tsitsiklis, Introduction to Linear Optimization, Athena Scientific, 1997.)








