Course Description
This course will focus on fundamental subjects in convexity, duality, and convex optimization algorithms. The aim is to develop the core analytical and algorithmic issues of continuous optimization, duality, and saddle point theory using a handful of unifying principles that can be easily visualized and readily …
This course will focus on fundamental subjects in convexity, duality, and convex optimization algorithms. The aim is to develop the core analytical and algorithmic issues of continuous optimization, duality, and saddle point theory using a handful of unifying principles that can be easily visualized and readily understood.
Course Info
Learning Resource Types
grading
Exams with Solutions
notes
Lecture Notes
assignment
Problem Sets
Problem Set Solutions
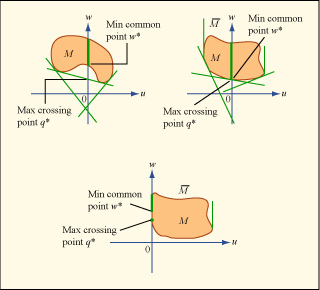
Min common/max crossing problems. See Lectures 8–9 for more information. (Image by MIT OpenCourseWare.)










