Course Description
Foundations and philosophical applications of Bayesian decision theory, game theory and theory of collective choice. Why should degrees of belief be probabilities? Is it always rational to maximize expected utility? If so, why and what is its utility? What is a solution to a game? What does a game-theoretic solution …
Foundations and philosophical applications of Bayesian decision theory, game theory and theory of collective choice. Why should degrees of belief be probabilities? Is it always rational to maximize expected utility? If so, why and what is its utility? What is a solution to a game? What does a game-theoretic solution concept such as Nash equilibrium say about how rational players will, or should, act in a game? How are the values and the actions of groups, institutions and societies related to the values and actions of the individuals that constitute them?
Course Info
Instructor
Departments
Learning Resource Types
grading
Exams
assignment
Problem Sets
assignment
Written Assignments
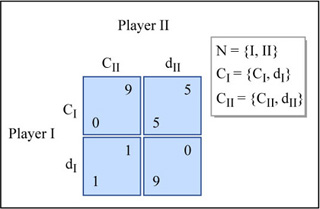
An example of a simple 2-person game in normal form. The numbers in each cell represent the respective utilities of the players. (Image by MIT OpenCourseWare.)










