Course Description
This course covers the mathematical techniques necessary for understanding of materials science and engineering topics such as energetics, materials structure and symmetry, materials response to applied fields, mechanics and physics of solids and soft materials. The class uses examples from the materials science and …
This course covers the mathematical techniques necessary for understanding of materials science and engineering topics such as energetics, materials structure and symmetry, materials response to applied fields, mechanics and physics of solids and soft materials. The class uses examples from the materials science and engineering core courses (3.012 and 3.014) to introduce mathematical concepts and materials-related problem solving skills. Topics include linear algebra and orthonormal basis, eigenvalues and eigenvectors, quadratic forms, tensor operations, symmetry operations, calculus of several variables, introduction to complex analysis, ordinary and partial differential equations, theory of distributions, and fourier analysis.
Course Info
Instructor
Departments
Learning Resource Types
notes
Lecture Notes
assignment_turned_in
Problem Set Solutions
assignment
Problem Sets
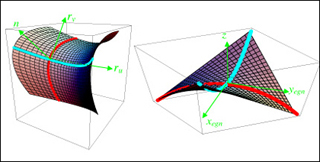
Parabolic approximation to a surface and local eigenframe. The surface on the left is a second-order approximation of a surface at the point where the coordinate axes are drawn. The surface has a local normal at that point which is related to the cross product of the two tangents of the coordinate curves that cross at the that point. The three directions define a coordinate system. The coordinate system can be translated so that the origin lies at the point where the surface is expanded and rotated so that the normal n coincides with the z-axis as in the right hand curve. (Image by Prof. W. Craig Carter.)










