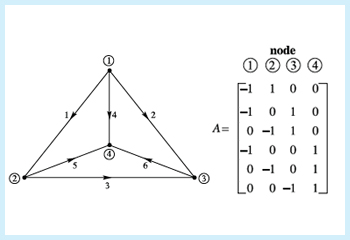
A graph and its edge-node incidence matrix.
Each component of a vector in Rn indicates a distance along one of the coordinate axes. This practice of dissecting a vector into directional components is an important one. In particular, it leads to the “least squares” method of fitting curves to collections of data. This unit also introduces matrix eigenvalues and eigenvectors. Many calculations become simpler when working with a basis of eigenvectors.
The determinant of a matrix is a number characterizing that matrix. This value is useful for determining whether a matrix is singular, computing its inverse, and more.
Looking for something specific in this course? The Resource Index compiles links to most course resources in a single page.








