Partial Differential Equation Assignment 1
Assignment 1 as a (PDF)
Problem 1
Prove that a Harmonic function with an interior maximum is constant.
Problem 2
Write out the laplacian in planepolar coordinates.
Problem 3
A Green’s function on 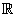 n is a harmonic function on
n is a harmonic function on 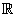 n \{0} which depends only on the radius (for example log r on
n \{0} which depends only on the radius (for example log r on 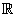 2). Find nontrivial Green’s functions for all dimensions.
2). Find nontrivial Green’s functions for all dimensions.
Problem 4
The heat equation for a function u: 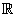 × [0, ∞) is
× [0, ∞) is 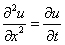 . Find all solutions of the form u = ƒ(t)g(x).
. Find all solutions of the form u = ƒ(t)g(x).
Problem 5
Find all solutions u of the heat equation on [0, 1] × [0, ∞) with the u = 0 on ({0} ∪ {1}) × [0, ∞).
Partial Differential Equation Assignment 2
Assignment 2 as a (PDF)
Problem 1
Let u be a function on the ball B1(0) ⊂ 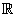 2 with ∫B1(0) |
2 with ∫B1(0) |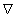 u|p <]infty for some constant p > 2. Show that u is holder continuous. [Hint: Use Morrey on ∫ 1.|
u|p <]infty for some constant p > 2. Show that u is holder continuous. [Hint: Use Morrey on ∫ 1.|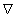 u|2 ]
u|2 ]
Problem 2
Let u: 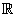 n →
n → 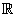 , and define OSCBr(x)u = supBr(x)u - infBr(x)u. Show that if there is some constant 0 < γ < 1 with
, and define OSCBr(x)u = supBr(x)u - infBr(x)u. Show that if there is some constant 0 < γ < 1 with
oscBr(x)u ≤ γ oscB2r(x)u
for all x and all r then u is Holder continuous.
Problem 3
Let L be a uniformly elliptic 2nd order operator in divergence form taking
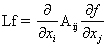
Let u be a function with Lu ≥ 0, and Φ: 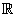 →
→ 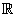 a function with Φ’, Φ" ≥ 0. Show that L(Φ(u))≥ 0.
a function with Φ’, Φ" ≥ 0. Show that L(Φ(u))≥ 0.
Problem 4
Let L be an operator as in question 3, and let u be an L harmonic function. Prove that |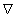 u|2 is holder contiuous. [This is likely to be difficult.]
u|2 is holder contiuous. [This is likely to be difficult.]








