Infinite Random Matrix Theory
As taught in: Fall 2004
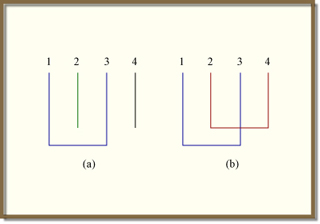
The power of infinite random matrix theory comes from being able to systematically identify and work with non-crossing partitions (as depicted on the left). The figure on the right depicts a crossing partition which becomes important when trying to understand the higher order terms which infinite random matrix theory cannot predict. (Figure by Prof. Alan Edleman.)
Instructors:
Prof. Moe Win
Prof. Alan Edelman
MIT Course Number:
18.338J / 16.394J
Level:
Graduate
