Course Description
This course is an elementary introduction to number theory with no algebraic prerequisites. Topics covered include primes, congruences, quadratic reciprocity, diophantine equations, irrational numbers, continued fractions, and partitions.
Course Info
Instructor
Departments
Learning Resource Types
assignment_turned_in
Problem Sets with Solutions
grading
Exams with Solutions
notes
Lecture Notes
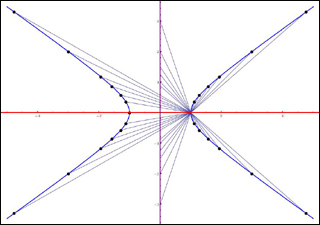
Some rational points on the hyperbola x^2 - 2y^2 = 1. The projection from away from (1,0) gives a bijection with the rational points on the y-axis, with the point (0,-m) going to x = (2m^2 + 1)/(2m^2 - 1), y = 2m/(2m^2 - 1). (Image by Abhinav Kumar.)








