These are final projects contributed by the students.
Student Projects
When is a minimal surface not area-minimizing? (PDF) (Courtesy of Nizameddin H. Ordulu. Used with permission.)
Characterizations of Complete Embedded Minimal Surfaces: Finite Curvature, Finite Topology, and Foliations (PDF) (Courtesy of Michael Nagle. Used with permission.)
Modern Examples of Complete Embedded Minimal Surfaces of Finite Total Curvature (PDF) (Courtesy of David Glasser. Used with permission.)
Minimal Surfaces as Isotropic Curves in C3: Associated minimal surfaces and the Bjoorling’s problem (PDF-2.2MB) (Courtesy of Kai-Wing Fung. Used with permission.)
List of Suggested Projects
The Mathematics of Soap Films: Explorations with Maple, by John Oprea
Work through Oprea’s book, choosing topics that you would like to explore. Give an expository account of the theory that you learn, do relevant exercises and try to make up your own exercises, or extend the ones that are there. Write maple routines to give pictures of the surfaces that you study. You may also want to do some of the soap film experiments that he lists. One possibility is to focus on the Weierstrass-Enneper representation (minimal surfaces from complex analytic data) and Björling’s problem (minimal surfaces from real-analytic curves and normal vector fields), but the best thing is to find what interests you, and study that.
Complete Embedded Minimal Surfaces in R3
Hoffman/Meeks’s discovery, for each g>0, of a complete embedded minimal surface in R3 of genus g with three points removed. Start with Hoffman’s expository article [2]. He gives a lovely introduction to minimal surfaces, and then describes how the computer graphics pictures they were able to generate led to the discovery. Read the article, and choose an aspect of it to follow up in more detail. You may want to learn more about Costa’s surface, or a higher genus example, all learn more about their proof. This project requires a little bit of complex analysis, specifically it uses the Weierstrass
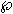
-function. This is not difficult to learn about, however, see Ahlfors p. 272. You may want to go to Geometry Analysis Numerics Graphics and both look at their pictures and use their software. From the mathscinet review “This superb survey article, illustrated by exceptional computer graphics fullcolor images, presents the history of the discovery of a family of embedded minimal surfaces with finite total curvature, the first such examples found since Euler described the catenoid minimal surface in 1740. The article sketches a fine historical account of the development of minimal surface theory by giving six equivalent definitions of minimality, leading to the Enneper-Weierstrass representation. In terms of this representation, C. Costa found an example which met all known criteria for embeddedness, but it was only after careful computer graphics investigation that the structure was understood well enough to lead to a proof of the embeddedness, as elaborated in the work of the author and W. H. Meeks, III. The article describes symmetry properties of Costa’s example and its generalization to embeddings of surfaces topologically equivalent to a sphere with arbitrarily many handles with three points removed. The computer graphics system developed by the author and James Hoffman played a crucial role in these discoveries and the article contains reflections on this process and the role of examples and models in mathematical creativity.”
When is a Minimal Surface Area Minimising?
Schwarz’s Theorem states that if M is a minimal surface in R3 spanning a curve C such that the image of M under its Gauss map contains a hemisphere of *S2 * then M is not area minimizing for C. A proof of this can be found in Oprea’s book. Conversely, under some reasonable assumptions, if the area of the Gauss image has area <2π then the surface is area minimising [1]. Investigate area minimisation for various regions of familiar minimal surfaces. The catenoid is a straightforward example, and is treated by Oprea, so this is the place to start. Oprea and [1] give different proofs of Schwarz’s Theorem; you should understand at least one of them, and you may want to compare them and give an outline of the argument of [1].
Gauss-Bonnet Theorem
This is not a theorem about minimal surfaces, but it is probably the most important theorem in surface theory, and it plays a role in projects 2 and 5 and is relevant to chapter 9 of Osserman, which is the last section we will cover in this course. For M a compact orientable surface, it states that
∫M K dA = 2πχ(M),
where χ(M) is the Euler characteristic of M. Do Carmo has a proof of it, as does Singer and Thorpe’s book. Give an account of the proof, and some applications.
Minimal Surfaces based on the Catenoid
From the mathscinet review of [3]: “In the present paper the authors first explain the flux formula for minimal surfaces, derive the catenoid equation, and present embedded minimal annuli. Then, complete embedded minimal surfaces with finite total curvature are discussed. The Weierstrass representations are given and beautiful computer graphics produced by J. T. Hoffman are provided. The authors also report on new finite total curvature examples. Then minimal surfaces foliated by convex curves in parallel planes are considered, and Shiffman’s beautiful theorems for this class of surfaces are presented. Furthermore, the authors treat Riemann’s examples of minimal surfaces foliated by circles and lines in parallel planes. Finally, embedded periodic minimal surfaces are discussed. They appear as interfaces in certain materials. This paper gives an excellent account of the progress in this very active, interesting area of minimal surface theory.” This paper is fairly accessible (though probably too long to study in its entirety), and includes some nice examples. However, it relies heavily on the Gauss-Bonnet Theorem, so you will need to either take this theorem on faith, or spend some time understanding its proof.
Gauss Maps for Surfaces in Rn
Osserman made major strides in the understanding of complete regular minimal surfaces in *R3, * which we will study in chapter 9. He made extensive use of the Gauss map, and was able to extend some of his results to surfaces in Rn using the generalised Gauss map. He describes this in chapter 12, and gives several references for further study. Give an expository account of his work.
Connections
Again, this is not a minimal surfaces project, but connections are very important in differential geometry. First learn about the Levi-Civita connection for surfaces in R3, then how it is defined intrinsically, and move on to higher dimensions and more abstract definitions. Do Carmo, and Singer and Thorpe are places to start; ask me for other references when you know what direction you want to take this project.
References
Barbosa, J. L., and M. Do Carmo. “On the size of a stable minimal surface in R3 Amer. J. Math. 98, no. 2 (1976): 515–528.
Hoffman, D. “The computer aided discovery of new embedded minimal surfaces.” The Mathematical Intelligencer 9, no. 3 (1987): 8–21.
Hoffman, D., and W. Meeks. “Minimal surfaces based on the catenoid.” Amer. Math. Monthly 97, no. 8 (1990): 702–730.








