Course Description
The course is a comprehensive introduction to the theory, algorithms and applications of integer optimization and is organized in four parts: formulations and relaxations, algebra and geometry of integer optimization, algorithms for integer optimization, and extensions of integer optimization.
Course Info
Learning Resource Types
assignment
Problem Sets
grading
Exams
notes
Lecture Notes
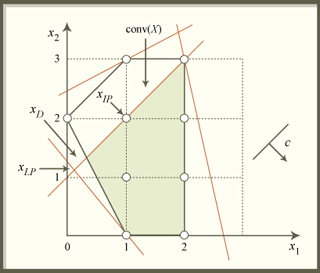
An example of Lagrangean duality, discussed in Lecture 8. (Image by Prof. Bertsimas.)










