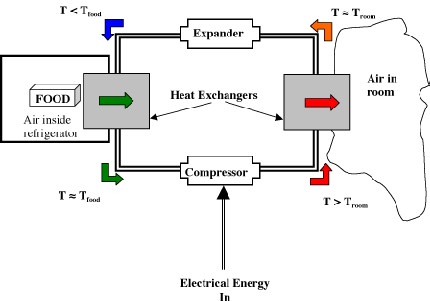
Thermodynamic cycles and heat engines(VW, S & B: Chapter 9)
This section of the course is devoted to describing the basic fundamentals of how various heat engines work (e.g. a refrigerator, an IC engine, a jet). You will also learn how to model these heat engines as thermodynamic cycles and how to apply the First Law of Thermodynamics to estimate thermal efficiency and work output as a function of pressures and temperatures at various points in the cycle. This is called ideal cycle analysis. The estimates you obtain from the analysis represent the best achievable performance that may be obtained from a heat engine. In reality, the performance of these systems will be somewhat less than the estimates obtained from ideal cycle analysis–you will learn how to make more realistic estimates in 16.050.
We will deal with only "air-standard" thermodynamic cycles, where we ignore the changes in properties of the working fluid brought about by the addition of fuel or the presence of combustion products (we do of course account for the heat release that occurs due to the combustion of the fuel-air mixture). In general this is a good assumption since in typical combustion applications the fuel accounts for only about 5% of the mass of the working fluid.
Q5.3 (PDF)
- The Otto Cycle (VW, S & B: 9.13)
-
Representation of the heat engine as a thermodynamic cycle.
-
Method for estimating thermal efficiency and work output (application of the First Law of Thermodynamics).
-
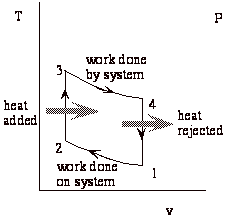
Net work done by system = work of expansion + work of compression (-)
-
While the above expression is accurate, it is not all that useful. We would like to put the expression in terms of the typical design parameters: the compression ratio (v1/v2 = v4/v3), and the heat added during combustion (qcomb. = cv(T3-T2)).
-
The thermal efficiency of the cycle is
- Brayton Cycle (VW, S & B: 9.8-9.9, 9.12)
-
Components of a gas turbine engine
-
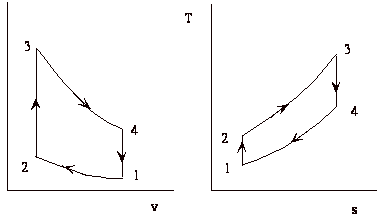
The thermodynamic cycle
-
Estimating the performance of the engine
-
heat added between 2-3 (combustor):
-
heat rejected between 4-1:
-
work done and thermal efficiency:
-
Rewriting equations in terms of design parameters:
- Generalized Representation of Thermodynamic Cycles (VW, S & B: 6.1)
-
To obtain data for an operating gas turbine engine (the one that provides power to MIT!) checkout the following links:
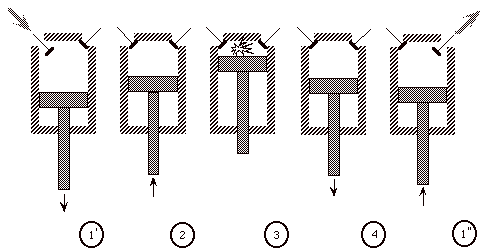
The Otto cycle is an idealization of a set of processes used by spark ignition internal combustion engines (2-stroke or 4-stroke cycles). These engines a) ingest a mixture of fuel and air, b) compress it, c) cause it to react, thus effectively adding heat through converting chemical energy into thermal energy, d) expand the combustion products, and then e) eject the combustion products and replace them with a new charge of fuel and air. The various steps are illustrated on page 9 of these notes.
We model all of these happenings by a thermodynamic cycle consisting of a set of processes all acting on a fixed mass of air contained in a piston-cylinder arrangement. The exhaust and intake processes are replaced by constant-volume cooling.
(Ingest mixture of fuel and air)
1’ - 2 Compress mixture quasi-statically and adiabatically
2 - 3 Ignite and burn mixture at constant volume (heat is added)
3 - 4 Expand mixture quasi-statically and adiabatically
4 - 1’’ Cool mixture at constant volume
(then repeat)
work ~ Force* distance ~ ![]()
fuel use ~ heat added ~ T3 - T2
efficiency ~ work out/fuel use
Both expansion and compression are adiabatic so
Dw = (u3 - u4) - (u2 - u1)
Assuming an ideal gas with constant cv
Dw = cv[(T3 - T4) - (T2 - T1)]
For a quasi-static, adiabatic process,
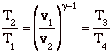 so
we can write the net work as
so
we can write the net work as
![]() we
also know that
we
also know that
![]() so
so
![]()
and finally, the desired result in terms of typical design parameters:
![]()
![]() so
so
![]()
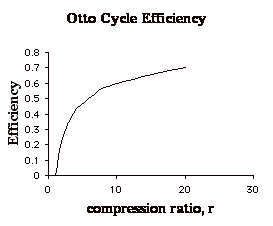
(Note that we could also rewrite this as:
![]() showing
that the efficiency of an Otto cycle depends only on the temperature ratio
of the compression process.)
showing
that the efficiency of an Otto cycle depends only on the temperature ratio
of the compression process.)
Q5.4 (PDF)
Homework 6 (PDF)
The Brayton cycle is an idealization of a set of thermodynamic processes used in gas turbine engines, whether for jet propulsion or for generation of electrical power.
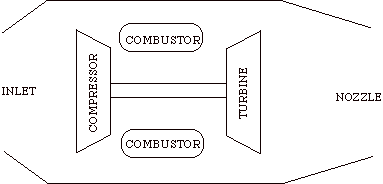
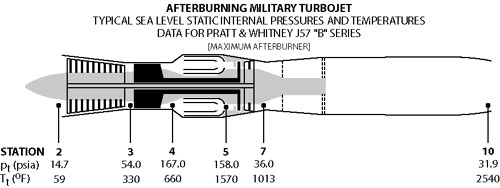
Schematics of typical military gas turbine engine: J57 turbojet with afterburning..
The cycle consists of four processes: a) quasi-static adiabatic compression in the inlet and compressor, b) constant pressure heat addition in the combustor, c) quasi-static adiabatic expansion in the turbine and exhaust nozzle, and finally d) constant pressure cooling to get the working fluid back to the initial condition.
1 - 2 Adiabatic, quasi-static compression in inlet and
compressor
2 - 3 Combust fuel at constant pressure (i.e. add heat)
3 - 4 Adiabatic, quasi-static expansion in turbine
a. take work out and use it to drive the compressor
b. take remaining work out and use it to accelerate fluid for jet
propulsion, or to turn a generator for electrical power generation.
4 - 1 Cool the air at constant pressure
Then repeat
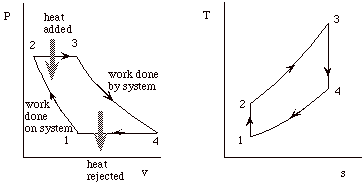
Our objective with the Brayton cycle is the same as for the Otto cycle. First to derive expressions for the net work and the thermal efficiency of the cycle, and then to manipulate these expressions to put them in terms of typical design parameters so that they will be more useful.
First, remember from the First Law we can show that for any cyclic process heat and work transfers are numerically equal
Du = q - w
ufinal = uinitial therefore Du = 0 and q = w or
![]()
This fact is often useful for solving thermodynamic cycles. For instance in this example, we would like to find the net work of the cycle and we could calculate this by taking the difference of the work done all the way around the cycle. Or, since Dq = Dw, we could just as well consider the difference between the heat added to the cycle in process 2-3, and the heat rejected by the cycle in process 4-1.
First Law in terms of enthalpy for an ideal gas undergoing a quasi-static process:
dq = dh - vdp or dq = cpdT - vdp
at constant pressure
qadded = cp DT or qadded = cp (T3 - T2)
similarly
qadded = cp DT or qrejected = cp (T4 - T1)
Dw = Dq = qadded - qrejected = cp[(T3 - T2) - (T4 - T1)]
hBrayton = (qadded - qrejected)/ qadded = [(T3 - T2) - (T4 - T1)]/(T3 - T2)
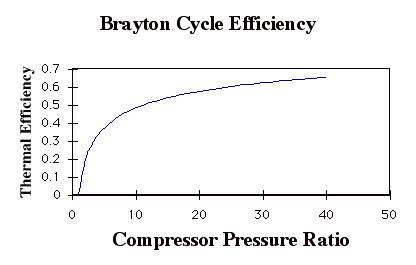
Again, while these expressions are accurate, they are not all that useful. We need to manipulate them to put them in terms of typical design parameters for gas turbine engines. For gas turbine engines the most useful design parameters to use for these equations are often the inlet temperature (T1), the compressor pressure ratio (p2/p1), and the maximum cycle temperature, the turbine inlet temperature (T3).
![]()
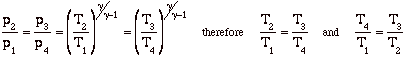
so
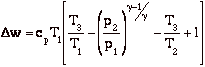 with
with 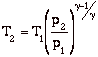
becomes
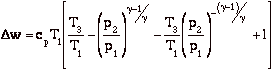
and for the efficiency
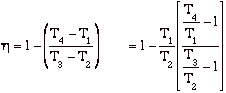 but
from above
but
from above ![]()
so
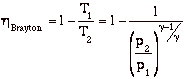
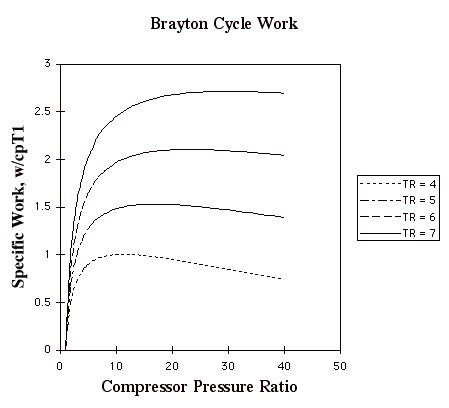
In the plot above, TR = T3/T1. Note that for a given turbine inlet temperature, T3, (which is set by material limits) there is a compressor pressure ratio that maximizes the work.
Q5.5 (PDF)
Q5.7 (PDF)
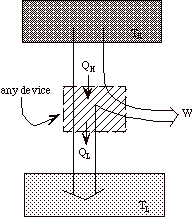
Note that heat engines can be represented generally as:
a transfer of heat from a high temperature reservoir to a device +
a rejection of heat from a device to a low temperature reservoir
+
net work done on surroundings
Homework 7 (PDF)