-
Consider a system composed of many bricks
-
Free vs. Reversible Expansions
-
Free expansion
-
Reversible expansion
- Reversibility, Irreversibility, and Lost Opportunity to Do Work

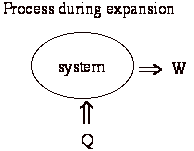
With these, we have the ability to obtain work by running a cycle between TL and TH.
What happens if put two bricks together? Applying the First Law:
|
|
cTH
+ cTL = 2cTM |
for a solid ![]()
therefore ![]()
We have lost the ability to get work out of these two bricks. Can we restore the situation:
a) without contact with outside? - No.
b) with contact from outside? - Yes, but we have to do work.
Overall process:
system is changed
outside (rest of universe) is unchanged
Composite: system + rest of universe is changed by putting bricks together.
The process is not reversible; That is there is no way to undo the change and leave no mark on the rest of the universe.
How do we measure this change?
1) Decreased ability to do work.
2) Energy? (This is conserved)
Measurement and characterization of this change is the subject of the Second Law of Thermodynamics. We will talk about this more later. For now let’s look at another example.
What is the difference between a free expansion of a gas and an isothermal expansion against a piston? To answer this we examine what we would have to do to reverse, i.e. to undo, the process.

Remove the partition and v1 Æ v2
The process is adiabatic (q = 0), and w = 0 since there is no motion of boundaries.
Therefore
Du = 0
For an ideal gas u = u(T) Æ T = constant = T1
State 1: v1, T1
State 2: v2, T1
q = w = 0 Æ no change in surroundings
To restore the system to the original state v2 Æ v1 at constant T, we compress isothermally by some external agency. We do this quasi-statically.

During the return process:
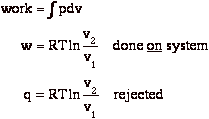
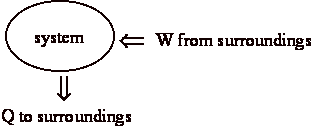
At end of the process:
a) system is back in initial state (no change)
b) surroundings (us) gave up work, w
c) surroundings received heat, q
Sum of all these processes is that we converted work, w, to heat, q.
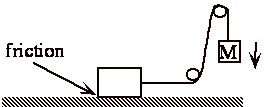
Same as if let weight fall and pull block along rough surface 100% W Æ Q.
Net effect: system same + surroundings changed = universe has changed.
The process is not reversible.
Now consider an isothermal expansion against an external pressure which is only dp less that the pressure in the system.
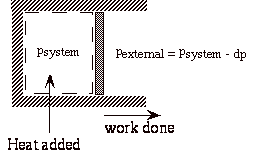
During expansion, the work done on the surroundings is
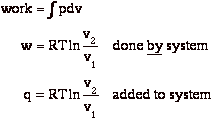
At the end of the isothermal expansion:
a) surroundings have received work
b) surroundings have given up heat
To restore the system to the original condition, we could put work back into system and reject heat to surroundings via a quasi-static isothermal compression just as we did following the free expansion.
Net result: system and surroundings back to initial state
The process is reversible.
Maximum work is achieved during a reversible expansion (or compression).
For example, suppose we have a thermally insulated cylinder that holds an ideal gas. The gas is contained by a thermally insulated massless piston with a stack of many small weights on top of it. Initially the system is in mechanical and thermal equilibrium.
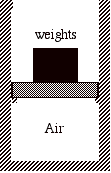
Consider the following three processes:
1) All of the weights are removed from the piston instantaneously and the gas expands until its volume is increased by a factor of four (a free expansion).
2) Half of the weight is removed from the piston instantaneously, the system is allowed to double in volume, and then the remaining half of the weight is instantaneously removed from the piston and the gas is allowed to expand until its volume is again doubled.
3) Each small weight is removed from the piston one at a time, so that the pressure inside the cylinder is always in equilibrium with the weight on top of the piston. When the last weight is removed, the volume has increased by a factor of four.
Maximum work (proportional to the area under these curves) is obtained for the quasi-static expansion. *Note that there is a direct inverse relationship between the amount of work received from a process and the degree of irreversibility.
Entropy as a Measure of Irreversibility (VW, S & B: 6.5-6.6, 7.1)
-
For a reversible (quasi-static), adiabatic process we can write the First Law as:
- For an irreversible case
- Entropy as a State Variable (VW, S & B: 7.10)
du = dq - pdv
or
cvdT = -pdv =
thus
We can think of the above equation as giving the fractional change in temperature in terms of the fractional change of volume for a reversible process. For instance, when the volume increases, the temperature decreases; the consequent reduction in thermal energy is equivalent to the work done on the surroundings. The quantities cv and R are scale factors for these two effects.
The volume increases with a smaller relative change in temperature and less work done on the surroundings. Recall the case of an adiabatic free expansion -- the temperature does not change at all, no work is done, but the volume increases.
We now introduce a property called entropy, and give it the symbol "s". We will use entropy change as a measure of how reversible a process is
Note that if the volume increases without a proportionate decrease in temperature, then s increases.
Since T and v are state variables, it follows from the above equation that s is as well. For the case of a thermally perfect gas then
or in situations with cv = constant
Also, writing
pv = RT as
we can get a relation for s(T,p) as well
So for the case of a thermally perfect gas then
or in situations with cp = constant
Homework 12 (PDF)
Second Law of Thermodynamics (VW, S & B: Chapter 6)
-
There exists for every system in equilibrium a property called entropy. (As with the Oth and 1st Laws, the 2nd Law starts by defining a useful property, "entropy".)
- The total entropy change (system + surroundings) is always greater than or equal to zero for any change of state of the system.
-
This is a statement that describes a useful behavior of this property "entropy". It turns out that the most efficient processes possible for converting energy from one form to another, are processes where the net entropy change of the system and the surroundings is zero. These processes represent limits - the best that can be done. In thermodynamics, propulsion, and power generation systems we often compare performance to these limits to measure how close to ideal a given process is.
-
Physically: Natural processes tend to go in certain directions, e.g. it is easier to mix two gases than to unmix them, and it is easier to bring two bricks initially at different temperatures to the same temperature than vice versa. Either direction satisfies the First Law. Second Law tells about the natural direction of processes and more importantly what the direction implies about the ability to do work with a system. (VW, S & B: 6.3-6.4)
-
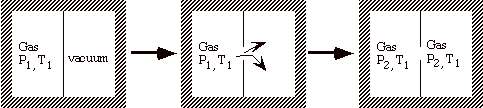
For example, consider an unrestrained expansion. We start with a thermally insulated (adiabatic) volume with a thin diaphragm in the middle. On one side of the diaphragm is vacuum, on the other is gas at some pressure. We open a hole in the diaphragm and the gas rushes through it. No work is done on surroundings, and there is no heat transfer, therefore there is no change in the energy of system (1st Law).
-
Do we ever see the reverse happen? (Only if we somehow devised a process where the surroundings supplied some work.)
-
The reverse is compatible, however, with the 1st Law. So there must be some other principle (like the 2nd Law) that governs the direction of processes.
-
Also note in the above example that some ability to do work has been lost. For instance we could have put a piston in the volume and allowed the expansion of the gas to do work to raise a weight.
-
If we carefully extract the maximum possible work from the system with a piston, then it is conceivable to think that we could reverse the process and put that work back into the system and everything (the system and the surroundings) would be back to the initial state.
-
But if we let the gas undergo a free expansion, we lose some ability to get work out of the system. The property that is used to measure the ‘change in ability to get work out of a system’ is the entropy.
-
For reversible processes (the most efficient processes possible), the net change in entropy in the universe (system + surroundings) is zero.
-
Phenomena that introduce irreversibility and inefficiency are: friction, heat transfer across finite temperature differences, free expansion.
Entropy is a function of the state of the system and can be found if any two properties of the system are known, e.g. s = s(p,T) or s = s (T,v) or s = s(p,v). We will discuss the equations that relate entropy to these other variables later in the class. (VW, S & B: 7.2-7.4)

-
System
-
State
-
Equilibrium
-
Pure substance
-
Intensive
-
Extensive
-
Specific volume
-
Thermally perfect gas
-
Heat
-
Adiabatic
-
Isobaric
-
Isothermal
-
Internal energy
-
Enthalpy
-
Static
-
Stagnation
-
Entropy
-
Reversible
-
Irreversible
-
Isentropic
-
Specific heat
-
Cycle