|
|
||
The important properties are:
The Pythagorean theorem (which is really our definition of distance as discussed below).
The addition theorems which are expressions for sin(a + b) and cos(a + b).
The half angle theorem (a consequence of the previous two).
All trigonometric functions depend only on the angle mod 2![]() .
.
The law of sines: in the triangle ABC, the ratio of the length AB and AC is
the ratio of the sines of the opposite angles:![]() .
This is just the fact that both ABsin B and ACsin C are equal to AH.
.
This is just the fact that both ABsin B and ACsin C are equal to AH.
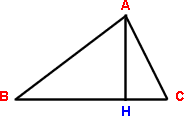
The law of cosines. (see Exercise 3.5)
The coordinates of the point on the unit circle at angle ![]() with center at the origin are (cos
with center at the origin are (cos![]() ,
sin
,
sin![]() )
which means y = sin
)
which means y = sin![]() ,
x = cos
,
x = cos![]() .
.
The tangent line to a circle with center at the origin through
(x, y) is perpendicular to the line from the center to (x, y) and points toward
the y axis in the first quadrant. Its direction is given by (-sin![]() ,
cos
,
cos![]() ).
).
All properties follow from the differential properties of the sine.
For the moment we assume
![]()
Then using
![]()
We get
![]()
These two statements combine to tell us that if we differentiate sin x twice we get -sin x; differentiating three times yields -cos x, and four times brings us back to where we started from with sin x.
And we have cos 0 = 1, sin 0 = 0.
And so we have sin 0 = 0, (sin 0)' = 1, (sin 0 )" = 0, (sin 0)''' = -1 and further derivatives repeat as (from the start 0 1 0 -1 0 1 0 -1 0 1 0 -1, etc) at argument 0.
This information determines a power series formula for the sine of x.
The constant term must be 0; the linear term x, the quadratic
term 0 the cubic term ![]() ,
and continuing around, all the even terms power terms must be 0, and the
odd
ones must alternate in sign and otherwise be just like those in the series
expansion of exp x.
,
and continuing around, all the even terms power terms must be 0, and the
odd
ones must alternate in sign and otherwise be just like those in the series
expansion of exp x.
All this follows because the monomial xk has all its derivatives 0 at x = 0 except the k-th which is k! We can therefore read off the power series for sine from the sequence of derivative values at 0.
We get
![]()
and similarly
![]()
which implies
exp ix = cos x + i sin x (A)
We can therefore use the properties of the exponential function to deduce the properties of the trigonometric functions.
For example, the addition theorem for sines and cosines can be deduced as follows
exp i(a+b) = cos (a + b) + i sin( a + b) = (exp ia) * (exp ib)
= cos a cos b – sin a sin b + i(cos a sin b + cos b sin a)
Identifying real and imaginary parts of these expressions gives the addition formulae.
Exercises:
2.10 Derive the formulae for sin x and cos x in terms of exp ix and exp(-ix), that follows from equation (A) above. Solution
2.11 Find expressions for (sin t/2)2 and (cos t/2)2 from the Pythagorean theorem and the cosine addition theorem. Solution
2.12 Set up a spreadsheet to compute the sin x for any inputed x. How many terms in the sin x power series expansion do you need to evaluate sin .5 to 8 decimal places? Solution
|
|