|
Home | 18.013A | Chapter 14 |
||
|
|
||
A surface in three dimensions is determined by one equation, which again we write as G = 0.
Suppose, again that we wish to find extrema of F on this surface.
This time ![]() F
can have no non-vanishing component in the plane tangent to the surface an extreme
point, exactly as in the previous case.
F
can have no non-vanishing component in the plane tangent to the surface an extreme
point, exactly as in the previous case.
This means that ![]() F
and
F
and ![]() G
must again point in the same direction.
G
must again point in the same direction.
We can observe that this implies that the cross product ![]() F
F![]()
![]() G
must be 0, and this vector equation gives us two independent component equations
that we can solve along with G = 0 to find the extrema.
G
must be 0, and this vector equation gives us two independent component equations
that we can solve along with G = 0 to find the extrema.
Also we can apply the Lagrange Multipliers approach exactly as before. This
time there are three components to all the vectors, so that the statement ![]() F
= c
F
= c![]() G
supplies us with three equations which, along with G = 0, is enough to determine
c and the coordinates of the extrema.
G
supplies us with three equations which, along with G = 0, is enough to determine
c and the coordinates of the extrema.
Again you must identify maxima and minima and distinguish merely local extrema from global ones at each extreme point.
When the surface is defined parametrically, you can reduce the problem by substitution to a two dimensional problem in the two parameters of the surface, with no restriction on the parameters. Finding critical points then involves solving the equations gotten by setting the partial derivatives of F with respect to the parameters to 0. The two dimensional Newton's Method of the last chapter can be used to do this for a numerical example.
Exercises:
14.3 Suppose we want to maximize xyz - x subject to the condition 2x2 + 4y2 + 3z2 = 6. Write equations for obeyed by x, y and z at critical points obtained by the cross product approach.
14.4 Write the equations for this same problem implied by the Lagrange Multipliers approach.
14.5 Suppose that on the surface defined by the parametric representation
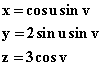
for 0 < u < 2![]() , 0 < v <
, 0 < v < ![]() .
.
We want to find the critical points of F, F = x4 - 2y2z2.
Find equations for same.
|
|