19.6 Differentiation with Respect to a Parameter

There is one other tool that can sometimes be used to evaluate anti-derivatives that works when certain convergence conditions hold.

Suppose we know the anti-derivative of g(x, y) where g is some differentiable function of the parameter y, as well as a function of x. Then we can deduce that an anti-derivative of is the derivative with respect to y of an anti-derivative of g.

For example, we know that an anti-derivative of We may then deduce that an anti-derivative of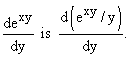

You can take higher derivatives with respect to y here as well. This allows you to deduce a formula for an anti-derivative of a function of the form x^k e^ax, by differentiating k times with respect to y and then setting y = a.

This method when it applies converts finding anti-derivatives to making appropriate differentiations. However, almost everything you can deduce this way can be gotten as well by integrating by parts judiciously.