|
Home | 18.013A | Chapter 23 |
||
|
|
||
Example 1
We begin by computing arc-length of our helix from ![]()
The parametric equations for P are x = cos s, y = sin s, and z = s. We therefore obtain
![]()
To compute arc-length we want to sum the lengths dl of each of our infinitesimal pieces of P.
Since we are integrating dl which is Tdl where T is the
unit vector in the direction tangent to P, which is the direction of ![]() ,
we can find dl from this by taking its dot product with the unit vector T,
which obeys
,
we can find dl from this by taking its dot product with the unit vector T,
which obeys ![]() .
.
We find then that arc length on P is given by
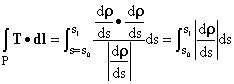
The integrand here is then the absolute value of 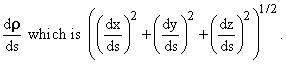
Here it is ![]()
The value of the integral and the arc-length of this helix is therefore ![]() .
.
Example 2
Compute the work done by the force of gravity when the naughty child throws
a stone of mass M out the window and it lands on the ground 30 feet below the
window. The work done here is given by the line integral over the path of the
stone of F![]() dl.
Since F = -Mgk, the integrand in the final ordinary integral ds becomes
dl.
Since F = -Mgk, the integrand in the final ordinary integral ds becomes ![]() and the work done by gravity is
and the work done by gravity is
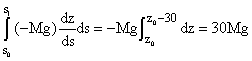
in appropriate units no matter what the path was, since the force is a gradient and the integral therefore path independent.
|
|