|
Home | 18.013A | Chapter 30 |
||
|
|
||
Suppose we have a power series in the variable x.
If it converges for some value of x, it will converge (by the comparison test) for any smaller value of x.
Thus the series will converge up to some maximum value of x, for which the ratio of successive terms becomes 1.
The maximum value of |x| at which the series converges is called its radius of convergence.
It is obvious that the same series represents a convergent and infinitely differentiable function for all values of x whose absolute value is strictly less than its radius of convergence.
On the other hand, there is generally a value of x in the complex plane at a distance given by the radius of convergence from the origin, at which the series is singular.
Thus, the radius of convergence of a series represents the distance in the complex plane from the expansion point to the nearest singularity of the function expanded.
For example, the geometric series in x (the series for (1-x)-1) blows up at x = 1 and 1 is its radius of convergence, and this behavior is typical of all power series.
This same function, (1-x)-1 can be expanded in a power series about argument -1. Since the distance between -1 and the singular point at x = 1 is 2, this series will have radius of convergence 2
![]()
Exercises:
30.6 Prove this statement by subtracting ![]() from the right hand side and dividing the result by
from the right hand side and dividing the result by ![]() ,
and rearranging the resulting statement.
,
and rearranging the resulting statement.
30.7 Figure out the comparable series for the same function expanded in powers of x + 3.
30.8 What is the radius of convergence of the exponential series expanded about the origin?
Another nice feature about power series is that if you start with the function f, you can deduce its series expansion about the point z by Taylor's theorem. f will have the expansion
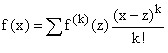
where f(k)(z) is the k-th derivative of f at argument z, and the sum is from k = 0 on.
Exercise 30.9 Find the series expansion for (1-x)-1 expanded about x = -3 by using Taylor's theorem, that is, by computing its derivatives there.
|
|