|
Home | 18.013A | Chapter 30 |
||
|
|
||
We have for the most part so far discussed what to do when confronted with a series. You can test its convergence, estimate its limit, and try to find the function it represents, if it is a power series.
Another important question is: how can you find the coefficients in a power series expansion of a given function about some expansion point?
We know from our study of Taylor series in Section 10.2 that the coefficient of the j-th term will be the j-th derivative of the function at the expansion point, divided by j factorial.
This is a useful fact, but not always useful enough, in part because it can be cumbersome to calculate or compute the higher derivatives of a complicated function.
Fortunately our standard functions can be defined in the complex plane, and in it we can give an integral representation of the coefficients of a power series, by using the residue theorem.
Suppose we have a function f(z) and wish to expand it in a series
about the point z'. We know that the integral of any function around a simple
closed path in the complex plane that surrounds an isolated singular point z'
(and no other singular point) of f is 2![]() i
times its residue at z', and the residue at z' is the coefficient of
i
times its residue at z', and the residue at z' is the coefficient of ![]() in the power series expansion of f at the point z'.
in the power series expansion of f at the point z'.
We can therefore deduce that the coefficient ![]() in the power series expansion of f(z) about z', which is the residue of
in the power series expansion of f(z) about z', which is the residue of ![]() at z = z', is
at z = z', is ![]() times the integral of
times the integral of ![]() on any simple closed path around z' that does not include any singular point
of f
on any simple closed path around z' that does not include any singular point
of f
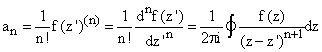
Integrals of this kind can be evaluated numerically for any n without great difficulty.
|
|