Mathematical Tools for Materials Scientists and Engineers
Learning to use Mathematica as a tool.
Starting up Mathematica
First you must locate or obtain Mathematica and permission to use it.
As an MIT student, you have an Athena account from which you can run Mathematica. There are a number of
ways to open and run a Mathematica session. Of course,you must first login, and then one method would be to:
1. open a shell
2. Add the Mathematica locker by typing: add math
2. At the shell prompt, type mathematica. (An interface to mathematica's software (properly known as Mathematica's kernel) called the Front End will open as well as menus and palettes).
3. Solve problems by defining symbols, performing mathematical operations, employing Mathematica's functions,defining your own functions, and graphically displaying results.
Also, as an MIT student, you are entitled to download a copy and license for $30 so that you can run Mathematica on your own computer. Instructions can be found at this URL: http://itinfo.mit.edu/article.php?id=6842
The colors on your sceen may not appear to be the same as what is presented in the lectures. I use my own style sheet, you may download my style sheet from here. Information on where to put the style sheet can be found below. Let's get started with some simple Mathematica commands.
If you are reading this in the Mathematica FrontEnd, then you can go ahead and familiarize yourself with some basics by executing the following lines which are Mathematica Input. Typically, Mathematica's FrontEnd asks Mathematica's Kernal to do its job of evaluating by hitting [SHIFT]—[ENTER] while the mouse in an "Input Cell." Input Cells can be identified with the ↓-thingy at the right. One can evaluate one or more cells by selecting their ↓-thingies and hitting [SHIFT]—[ENTER].
Try executing the cells below. Try to guess what the output might be or represent—and observe carefully whether Mathematica is doing what you would anticipate. Notice that answers can depend on the history of commands that precede it.
Assigning values to symbols
In[190]:=
Out[190]=
In[191]:=
Out[191]=
In[192]:=
Out[192]=
In[193]:=
Out[193]=
In[194]:=
Out[194]=
In[195]:=
Out[195]=
In[196]:=
Out[196]=
In[197]:=
Out[197]=
Differences between exact expressions and numerical expressions
In[198]:=
Out[198]=
In[199]:=
Out[199]=
In[200]:=
Out[200]=
In[201]:=
Out[201]=
In[202]:=
Out[202]=
Distinction between Equality (= = ) and Assignment (=)
In[203]:=
Out[203]=
In[204]:=
Out[204]=
Clearing Variables
In[205]:=
Global`a
In[206]:=
In[207]:=
Global`a
In[208]:=
Out[208]=
clearing all defined variables
In[209]:=
Mathematica Functions
In[210]:=
Out[210]=
In[211]:=
Out[211]=
In[212]:=
Out[212]=
Alternative Syntax for Functions //
In[213]:=
Out[213]=
In[214]:=
Out[214]=
Mathematica Operations on expressions
In[215]:=
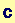
![AnotherVersionofC = Expand[c]](HTMLFiles/index_2.gif)
Out[215]=
Out[216]=
In[217]:=
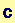
![Simplify[AnotherVersionofC]](HTMLFiles/index_4.gif)
Out[217]=
Out[218]=
In[219]:=
Out[219]=
Calculus
In[220]:=
Out[220]=
In[221]:=
Out[221]=
Getting information (part 1)
In[222]:=
Calculus, continued
In[223]:=
Out[223]=
In[224]:=
Out[224]=
In[225]:=
Out[225]=
In[226]:=
Out[226]=
In[227]:=
Out[227]=
In[228]:=
Out[228]=
In[229]:=
In[230]:=
Out[230]=
In[231]:=

![AnotherVersionofIntegralofC = Integrate[AnotherVersionofC, x]](HTMLFiles/index_6.gif)
Out[231]=
Out[232]=
In[233]:=
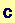
![D[IntegralofC, x]](HTMLFiles/index_8.gif)
Out[233]=
Out[234]=
In[235]:=
![Factor[c]](HTMLFiles/index_9.gif)
![Simplify[D[IntegralofC, x]]](HTMLFiles/index_10.gif)
Out[235]=
Out[236]=
Plotting Functions
In[237]:=
![[Graphics:HTMLFiles/index_11.gif]](HTMLFiles/index_11.gif)
Out[237]=
In[238]:=
![[Graphics:HTMLFiles/index_12.gif]](HTMLFiles/index_12.gif)
Out[238]=
In[239]:=
![[Graphics:HTMLFiles/index_13.gif]](HTMLFiles/index_13.gif)
Out[239]=
In[240]:=
Out[240]=
In[241]:=
![[Graphics:HTMLFiles/index_14.gif]](HTMLFiles/index_14.gif)
Out[241]=
Lists {} and Matrices {{}} (Lists of Lists)
Note that we have already used lists in Plot and in Integrate
In[242]:=
In[243]:=
Out[243]=
In[244]:=
Out[244]=
In[245]:=
Out[245]=
In[246]:=

![AList[[2]]](HTMLFiles/index_16.gif)
Out[246]=
Out[247]=
In[248]:=

![AList[[{3, 6}]]](HTMLFiles/index_18.gif)
Out[248]=
Out[249]=
In[250]:=

![AList[[-2]]](HTMLFiles/index_20.gif)
Out[250]=
Out[251]=
In[252]:=
Out[252]=
In[253]:=
Out[253]=
In[254]:=
Out[254]=
In[255]:=
Out[255]=
In[256]:=
Out[256]=
In[257]:=
Out[257]=
In[258]:=
Out[258]=
In[259]:=
Out[259]//MatrixForm=
In[260]:=
In[261]:=
Out[261]=
In[262]:=
Out[262]=
In[263]:=
Out[263]=
In[264]:=
Out[264]=
In[265]:=
Out[265]=
In[266]:=
Out[266]=
Selecting the odd numbered columns from a matrix
In[267]:=
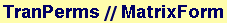
![TranPerms[[All, Select[IntList, OddQ]]]//MatrixForm](HTMLFiles/index_22.gif)
Out[267]//MatrixForm=
Out[268]//MatrixForm=
Rules → and Replacement /.
In[269]:=
Out[269]=
In[270]:=
Out[270]=
In[271]:=

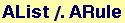
Out[271]=
Out[272]=
In[273]:=
Out[273]=
In[274]:=
Out[274]=
In[275]:=
In[276]:=
Out[276]=
In[277]:=
Out[277]=
In[278]:=
Out[278]=
Getting Help
Several methods of getting help can be found in the above examples.
1. Mathematica indicated that a possible type might have occured and returned a "warning message" with a link to Mathematica's Help Browser. Some people find typo and spelling warnings to be annoying. Spelling warnings can be disabled by typing Off[General::spell1]. However, prudence and experience show that undiscovered typos can be even more annoying.
2. Typing ?ExpIntegralEi returned information about the symbol ExpIntegralEi. Typing ??FunctionName gives even more information—try ??Plot. Wildcards can also by used as demonstrated below.
In[279]:=
| System` |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| DiscreteMath`Combinatorica` |
|
|
| Statistics`DescriptiveStatistics` |
|
|
Each of the above is linked to Mathematica's Help Browser.
3. Typing Options[Plot] returned a list of options that can be adjusted by the user until the result (in this case the appearance) of the plot is satisfactory.
Mathematica's Help Browser is a very useful tool and will probably become a primary resource for students. It contains good tutorials and demonstrations that can be copied and pasted. It has very good and concise descriptions of mathematics; in fact, exploring the Help Browser is a good way to explore mathematics as well as Mathematica. For instance , the discussion of "Combinatorial Functions" under Mathematical Functions ▸ Combinitorial has summarizes some useful information about counting and parttioning of sets.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/index_11.gif]](HTMLFiles/index_11.gif)
![[Graphics:HTMLFiles/index_12.gif]](HTMLFiles/index_12.gif)
![[Graphics:HTMLFiles/index_13.gif]](HTMLFiles/index_13.gif)
![[Graphics:HTMLFiles/index_14.gif]](HTMLFiles/index_14.gif)
![]()
![]()
![]()
![]()
![]()
![]()