Introduction to Mathematica, Part II
Mathematica can be used in the same fashion as a traditional programming language, such a fortran or C. For frequently used programs or computationally intensive applications, Mathematica is not the best programming language choice, but it can be very effective as a way to test out ideas or generate a single numerical result.
Evaluating a sequence of instrutions (;;;)
In[1]:=
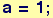
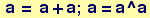
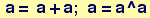
Out[2]=
Out[3]=
Note above that line breaks without ";" are points where the instructions get executed. This three-line sequence produces two lines of output and the instructions get executed sequentially.
In[4]:=
Loops
In[5]:=
In[6]:=
In[7]:=
Out[7]=
In this case, Do does not produce screen output. The following will and is a simple illustration of how formatted output can be programmed:
In[8]:=
In[9]:=
In[10]:=
In[11]:=
In[12]:=
In[13]:=
In[14]:=
In[15]:=
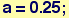
![Table[{i, a = 2a ; a = a^a}, {i, 1, 4}]](HTMLFiles/Lecture-03_5.gif)
Out[16]=
Note above that we have asked Mathematica to create a list of two-element lists...
In[17]:=
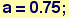
![Table[{i, a = 2a ; a = a^a}, {i, 1, 4}]](HTMLFiles/Lecture-03_7.gif)
Out[18]=
In[19]:=
Out[19]=
In the instruction above, note that the variable "datatable" is a list. In Mathematica, variables can be numbers, expressions, lists, plots, ... We will see that this feature is very useful.
In[20]:=
![[Graphics:HTMLFiles/Lecture-03_8.gif]](HTMLFiles/Lecture-03_8.gif)
Out[20]=
In[21]:=
Out[21]=
Note that the options are written as Rules.
In[22]:=
![[Graphics:HTMLFiles/Lecture-03_9.gif]](HTMLFiles/Lecture-03_9.gif)
Out[22]=
In[23]:=
In[24]:=
Out[24]=
By going into the Help Browser, you can see that the output of FindMinimum is a list, the first element of which is the functions minimum value, and the second is a Rule specifing where the minimum occurs.
Lets try and do the above the hard way. I will use Nest to recursively apply the function 4 times (I am just using a shorthand here, we can ignore the use of Nest for this course...). You can see that it works. Don't worry about it, but if you want to know about it, use the Help Browser to get information about Nest and Pure Functions.
In[25]:=
In[26]:=
Out[26]=
Take it derivative and set equal to zero...
In[27]:=
Out[27]=
Finding the zero of this will not be easy.... but FindRoot claims it can do it...
In[28]:=
Out[28]=
Local Variables
In the above, the values of a and dx are used repeatly—however, if we are only interested in the resulting minimum, their final values have little meaning or importance. Suppose, we use the value of a or dx without clearing—what will the value be?
In[29]:=
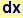
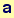
Out[29]=
Out[30]=
In[31]:=
As this could cause problems if a is used in a function call, say Sin[2 π a], it is a good idea to localize variables.
In[32]:=
In[33]:=
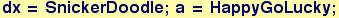
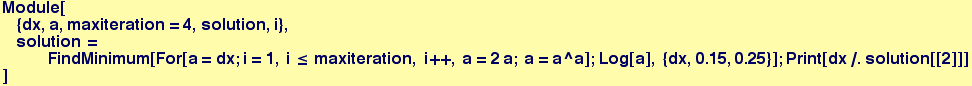
In[35]:=
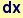
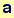

Out[35]=
Out[36]=
Out[37]=
Switches: If, Which
In[38]:=
In[39]:=
Out[39]=
In[40]:=
In[41]:=
The above program is ok, but not very useful because it only works for the current value of a. It would be more useful to have something that worked for any value of a and could use it over again—that is, turn it into a tool. This involves patterns and function definitions.
Patterns (_)
Patterns and Pattern Replacement are probably one of the most powerful features of Mathematica. The underscore _ stands for a pattern, a symbol x with an underscore (x_) is recognized as anypattern that matches x. Here are some examples.
In[42]:=
Out[42]=
In[43]:=
Out[43]=
Here's a way to put the last input command into words: Search list AList for any pattern that matches "2 × anything" and replace "2 × anything" with a, then output the new AList. Study the following examples carefully:
In[44]:=
In[45]:=
Out[45]=
In[46]:=
Out[46]=
A qualifier on a pattern can be used to restrict which expressions will match the pattern:
In[47]:=
Out[47]=
The third member of this result may be a bit surprising; it has to do with the way Mathematica internalizes expressions. In this case it represents the fraction as a and it performs the replacement on the exponent (note that it must treat the "-" sign independently of the "1", as it returns "-One" rather than "One"…).
_ all by itself stands for anything. x_ also stands for anything, but gives anything a name for later use.
In[48]:=
Out[48]=
This is not very useful and it really is doing what you asked for—the first thing it found was AList itself and replaced AList with AppleDumplings.
x^n_ stands for x to any power, and the power can be refered to as n; x_^n_ stands for any expression raised to a power. We can use these ideas to find rules that look like derivatives (this is not a good way to make a symbolic derivative, but it is illustrative):
In[49]:=
Out[49]=
In[50]:=
Out[50]=
This is ok, but it has least two problems. The first is that it would be nice to have the rule work for any polynomial...
In[51]:=
In[52]:=
Out[52]=
In[53]:=
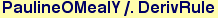
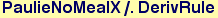
Out[53]=
Out[54]=
Another problem is that it will not work for first-order and zeroeth-order terms...
In[55]:=
Out[55]=
In[56]:=
Out[56]=
This could be fixed, but it would be much easier to do so by defining functions of a pattern.
It is also possible to have a pattern apply conditionally using a condition. Here is an example that pulls out cases where the first member of a pair of numbers is less than the second.
In[57]:=
In[58]:=
Out[58]=
Defining Functions with Patterns
Defining functions with patterns probably combines the most useful aspects of Mathematica. Define a function that takes patten matching x as its first argument and an argument matching n as its second argument and returns x to the power:
In[59]:=
In[60]:=
![f[2, 3]](HTMLFiles/Lecture-03_19.gif)
![f[y, z]](HTMLFiles/Lecture-03_20.gif)
Out[60]=
Out[61]=
This works fine, but suppose we had defined x ahead of time
In[62]:=
Out[62]=
In[63]:=
RHS evaluated, it is x^(second argument) which is currently 4^(second argument)
In[64]:=
Out[64]=
In[65]:=
Out[65]=
Delayed Assignmet (:=)
The problem with the above functions is that the evaluation is made immediately. For a function, the argument serves as a placeholder for a future calculation. You do not wish to have the right–hand–side evaluated until the actual values of left–hand–side are specified. The remedy is to use delayed assignment :=
In[66]:=
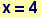

Out[66]=
Out[67]=
In[68]:=
In[69]:=
Out[69]=
In[70]:=
Out[70]=
In[71]:=
Out[71]=
In[72]:=
Out[72]=
In[73]:=
Functional Programming with Rules
The canonical programming example is the factorial function n! = (n)×(n-1) ×(n-2)×…×(1) where 0! ≡ 1; here is a reasonably clever way to use the fact that (n+1)! = (n+1)×n!
In[74]:=
This is part of definition, try it out...
In[75]:=
Out[75]=
Ooops, Mathematica does not know when to quit. Add the second part of the definition.
In[76]:=
In[77]:=
Out[77]=
In[78]:=
Out[78]=
In[79]:=
Out[79]=
In[80]:=
Out[80]=
In[81]:=
Out[81]=
Using immediate assignment in a function: spending memory to buy time.
In[82]:=
In[83]:=
Out[83]=
In[84]:=
Out[84]=
In[85]:=
Functions and Patterns with Restricted Rules
The factorial function is pretty good, but not foolproof:
In[86]:=
In[4]:=
In[5]:=
Out[5]=
The remedy is to restrict the pattern:
In[6]:=
In[7]:=
In[8]:=
Out[8]=
Still not perfect:
In[9]:=
Out[9]=
In[10]:=
In[11]:=
In[12]:=
Out[12]=
In[13]:=
Out[13]=
As a last example, let's define the Sign function. It should be -1 when its argument is negative, 0 when its argument is zero, and +1 when its argument is positive. There are lots of ways to write this function, there is no best way. Whatever works is good.
In[14]:=
In[15]:=
In[16]:=
![[Graphics:HTMLFiles/Lecture-03_23.gif]](HTMLFiles/Lecture-03_23.gif)
Out[16]=
In[17]:=
![[Graphics:HTMLFiles/Lecture-03_24.gif]](HTMLFiles/Lecture-03_24.gif)
Out[17]=
![]()
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/Lecture-03_8.gif]](HTMLFiles/Lecture-03_8.gif)
![[Graphics:HTMLFiles/Lecture-03_9.gif]](HTMLFiles/Lecture-03_9.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/Lecture-03_23.gif]](HTMLFiles/Lecture-03_23.gif)
![[Graphics:HTMLFiles/Lecture-03_24.gif]](HTMLFiles/Lecture-03_24.gif)