Complex Numbers/Complex Plane

Background

The positive square root of -1

$\mathrm{imaginary}=\mathrm{Sqrt}\left[-1\right]$

$i$

$\left(-\mathrm{imaginary}\right)^2$

$-1$

Complex numbers are composed of a real part + an imaginary part

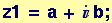
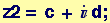
Simple operations on complex numbers

$\mathrm{compadd}=\mathrm{z1}+\mathrm{z2};$

$\mathrm{compmult}=\mathrm{z1}*\mathrm{z2};$

$\mathrm{Simplify}\left[\mathrm{compmult},a\in \mathrm{Reals}\&\&b\in \mathrm{Reals}\&\&c\in \mathrm{Reals}\&\&d\in \mathrm{Reals}\right]$

$\left(a+ib\right)\left(c+id\right)$

Mathematica does not assume that symbols are necessarily real...

$-\mathrm{Im}\left[b\right]-\mathrm{Im}\left[d\right]+\mathrm{Re}\left[a+c\right]$

$\mathrm{Im}\left[a+c\right]+\mathrm{Re}\left[b\right]+\mathrm{Re}\left[d\right]$

However, the Mathematica function ComplexExpand does assume that the variables are real....

$\mathrm{ComplexExpand}\left[\mathrm{Re}\left[\mathrm{compadd}\right]\right]$

$a+c$

$\mathrm{ComplexExpand}\left[\mathrm{Im}\left[\mathrm{compadd}\right]\right]$

$b+d$

$\mathrm{ComplexExpand}\left[\mathrm{Re}\left[\mathrm{z1}/\mathrm{z2}\right]\right]$

$\frac{ac}{c^2+d^2}+\frac{bd}{c^2+d^2}$

$\mathrm{ComplexExpand}\left[\mathrm{compmult}\right]$

$ac-bd+i\left(bc+ad\right)$

$a^3-3a{b}^2$

$3a^{2}b-b^3$

Function to convert to Polar Form

$\mathrm{Pform}\left[\text{z\_}\right]:=\mathrm{Abs}\left[z\right]\mathrm{Exp}\left[i\mathrm{Arg}\left[z\right]\right]$

Note: the function Arg[z] returns an angle in the range -π to π which measures the inclination of z with respect to the +Re axis in the complex plane.

$\mathrm{Pform}\left[\mathrm{z1}\right]$

$e^{i\mathrm{Arg}\left[a+ib\right]}\mathrm{Abs}\left[a+ib\right]$

$\mathrm{Pform}\left[\mathrm{z1}/.\left\{a\to 2,b\to -\pi \right\}\right]$

$e^{-i\mathrm{ArcTan}\left[\frac{\pi }{2}\right]}\sqrt{4+{\pi }^2}$

$\mathrm{ComplexExpand}\left[\mathrm{Pform}\left[\mathrm{z1}\right]\right]$

$\sqrt{a^2+b^2}\mathrm{Cos}\left[\mathrm{Arg}\left[a+ib\right]\right]+i\sqrt{a^2+b^2}\mathrm{Sin}\left[\mathrm{Arg}\left[a+ib\right]\right]$

Numerical Precision and Complex Rounding

$\mathrm{ExactlyOne}=\mathrm{Exp}\left[2\pi i\right]$

$1$

$\mathrm{NumericallyOne}=\mathrm{Exp}\left[N\left[2\pi i\right]\right]$

$1.\text{}-2.449293598294706\times {10}^{-16}i$

$\mathrm{Chop}\left[\mathrm{NumericallyOne}\right]$

$1.$

$\mathrm{Round}\left[\mathrm{NumericallyOne}\right]$

$1$

$\mathrm{ExactlyI}=\mathrm{Exp}\left[\pi i/2\right]$

$i$

$\mathrm{NumericallyI}=\mathrm{Exp}\left[N\left[\pi i/2\right]\right]$

$6.123233995736766\times {10}^{-17}+1.i$

$\mathrm{Round}\left[\mathrm{NumericallyI}\right]$

$i$

$\mathrm{Chop}\left[\mathrm{NumericallyI}\right]$

$1.i$

$\mathrm{ExactlyOnePlusI}=\mathrm{ComplexExpand}\left[\sqrt{2}\mathrm{Exp}\left[\pi i/4\right]\right]$

$1+i$

$\mathrm{NumericallyOnePlusI}=\mathrm{ComplexExpand}\left[\sqrt{2}\mathrm{Exp}\left[N\left[\pi i/4\right]\right]\right]$

$1.\text{}+1.0000000000000002i$

$\mathrm{Chop}\left[\mathrm{NumericallyOnePlusI}\right]$

$1.\text{}+1.0000000000000002i$

$\mathrm{Round}\left[\mathrm{NumericallyOnePlusI}\right]$

$1+i$

$\mathrm{Re}\left[\mathrm{NumericallyOnePlusI}\right]$

$1.$

$\mathrm{Im}\left[\mathrm{NumericallyOnePlusI}\right]$

$1.0000000000000002$

Roots to Polynomial Equations

Complex numbers frequently appear in the solution of roots to polynomial equations:

$\mathrm{sols}=\mathrm{Solve}\left[\left(x^4-x^3+x+1\right)⩵0,x\right]$

$\left\{\left\{x\to \frac{1}{4}-\frac{i\sqrt{7}}{4}-\frac{1}{2}\sqrt{\frac{5}{2}-\frac{i\sqrt{7}}{2}}\right\},\left\{x\to \frac{1}{4}-\frac{i\sqrt{7}}{4}+\frac{1}{2}\sqrt{\frac{5}{2}-\frac{i\sqrt{7}}{2}}\right\},\left\{x\to \frac{1}{4}+\frac{i\sqrt{7}}{4}-\frac{1}{2}\sqrt{\frac{5}{2}+\frac{i\sqrt{7}}{2}}\right\},\left\{x\to \frac{1}{4}+\frac{i\sqrt{7}}{4}+\frac{1}{2}\sqrt{\frac{5}{2}+\frac{i\sqrt{7}}{2}}\right\}\right\}$

The next statement produces a list of the complex solutions of the polynomial:

$x/.\mathrm{sols}$

$\left\{\frac{1}{4}-\frac{i\sqrt{7}}{4}-\frac{1}{2}\sqrt{\frac{5}{2}-\frac{i\sqrt{7}}{2}},\frac{1}{4}-\frac{i\sqrt{7}}{4}+\frac{1}{2}\sqrt{\frac{5}{2}-\frac{i\sqrt{7}}{2}},\frac{1}{4}+\frac{i\sqrt{7}}{4}-\frac{1}{2}\sqrt{\frac{5}{2}+\frac{i\sqrt{7}}{2}},\frac{1}{4}+\frac{i\sqrt{7}}{4}+\frac{1}{2}\sqrt{\frac{5}{2}+\frac{i\sqrt{7}}{2}}\right\}$

$\mathrm{Im}\left[x/.\mathrm{sols}\right]$

$\left\{-\frac{\sqrt{7}}{4}+\mathrm{Im}\left[-\frac{1}{2}\sqrt{\frac{5}{2}-\frac{i\sqrt{7}}{2}}\right],-\frac{\sqrt{7}}{4}+\mathrm{Im}\left[\frac{1}{2}\sqrt{\frac{5}{2}-\frac{i\sqrt{7}}{2}}\right],\frac{\sqrt{7}}{4}+\mathrm{Im}\left[-\frac{1}{2}\sqrt{\frac{5}{2}+\frac{i\sqrt{7}}{2}}\right],\frac{\sqrt{7}}{4}+\mathrm{Im}\left[\frac{1}{2}\sqrt{\frac{5}{2}+\frac{i\sqrt{7}}{2}}\right]\right\}$

$\mathrm{ComplexExpand}\left[\mathrm{Im}\left[x/.\mathrm{sols}\right]\right]$

$\left\{-\frac{\sqrt{7}}{4}+\frac{\mathrm{Sin}\left[\frac{1}{2}\mathrm{ArcTan}\left[\frac{\sqrt{7}}{5}\right]\right]}{2^{1/4}},-\frac{\sqrt{7}}{4}-\frac{\mathrm{Sin}\left[\frac{1}{2}\mathrm{ArcTan}\left[\frac{\sqrt{7}}{5}\right]\right]}{2^{1/4}},\frac{\sqrt{7}}{4}-\frac{\mathrm{Sin}\left[\frac{1}{2}\mathrm{ArcTan}\left[\frac{\sqrt{7}}{5}\right]\right]}{2^{1/4}},\frac{\sqrt{7}}{4}+\frac{\mathrm{Sin}\left[\frac{1}{2}\mathrm{ArcTan}\left[\frac{\sqrt{7}}{5}\right]\right]}{2^{1/4}}\right\}$

$\mathrm{ComplexExpand}\left[\mathrm{Im}\left[x/.\mathrm{sols}\right]\right]//N$

$\left\{-0.458821464672557,-0.8640541908597383,0.458821464672557,0.8640541908597383\right\}$

$\mathrm{ComplexExpand}\left[\mathrm{Re}\left[x/.\mathrm{sols}\right]\right]//N$

$\left\{-0.5661209411559501,1.0661209411559502,-0.5661209411559501,1.0661209411559502\right\}$

Generalize the above to a family of solutions: find b such that imaginary part of the solution vanishes

$\mathrm{bsols}=\mathrm{Solve}\left[\left(x^4-x^3+b*x+1\right)⩵0,x\right]$

This will give a list of rules that can be used to find solutions;as "b" is unspecified the rules depend on the symbol "b"

$\mathrm{General}\text{::}\mathrm{spell1}:\text{Possible spelling error: new symbol name "}\mathrm{bsols}\text{" is similar to existing symbol "}\mathrm{sols}\text{".}\mathrm{More\dots }$

$\left\{\left\{x\to \frac{1}{4}-\frac{1}{2}\surd \left(\frac{1}{4}+\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}+\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}\right)-\frac{1}{2}\surd \left(\frac{1}{2}-\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}-\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}-\frac{1-8b}{4\sqrt{\frac{1}{4}+\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}+\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}}}\right)\right\},\left\{x\to \frac{1}{4}-\frac{1}{2}\surd \left(\frac{1}{4}+\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}+\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}\right)+\frac{1}{2}\surd \left(\frac{1}{2}-\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}-\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}-\frac{1-8b}{4\sqrt{\frac{1}{4}+\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}+\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}}}\right)\right\},\left\{x\to \frac{1}{4}+\frac{1}{2}\surd \left(\frac{1}{4}+\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}+\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}\right)-\frac{1}{2}\surd \left(\frac{1}{2}-\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}-\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}+\frac{1-8b}{4\sqrt{\frac{1}{4}+\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}+\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}}}\right)\right\},\left\{x\to \frac{1}{4}+\frac{1}{2}\surd \left(\frac{1}{4}+\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}+\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}\right)+\frac{1}{2}\surd \left(\frac{1}{2}-\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}-\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}+\frac{1-8b}{4\sqrt{\frac{1}{4}+\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}+\frac{{\left(9+9b^2+\sqrt{3}\sqrt{-229-192b+6b^2-4b^3+27b^4}\right)}^{1/3}}{2^{1/3}{3}^{2/3}}}}\right)\right\}\right\}$

Because it is a long set of rules and hard to follow, let's look at the form of bsols:

$\mathrm{Dimensions}\left[\mathrm{bsols}\right]$

$\left\{4,1\right\}$

Short produces a very abbreviated form of the solution… in this case limited to 3 lines by the optional parameter.

$\mathrm{Short}\left[\mathrm{bsols},3\right]$

$\left\{\left\{x\to \frac{1}{4}-\frac{1}{2}\sqrt{\frac{1}{4}+\frac{1}{1}+\frac{1}{1}}-\frac{1}{2}\sqrt{\frac{1}{2}-\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(1\right)}^{1/3}}-\frac{1}{2^{1}1}-\frac{1-8b}{4\sqrt{\frac{1}{4}+\frac{111}{{1}^{1}}+\frac{{\left(1\right)}^{1/3}}{2^{111}1}}}}\right\},3\right\}$

So we see that bsols is a list of length 4 of list containing one rule. (Solutions to equations are always this way, it is a list of the number of solutions, each member being a rule for each variable that is solved for...)

In our case of one variable, the extra layer of lists is not terribly useful, one way to get rid of the extra layers is to use Flatten:

$\left\{4\right\}$

$\left\{x\to \frac{1}{4}-\frac{1}{2}\sqrt{\frac{1}{4}+\frac{1}{1}+\frac{1}{1}}-\frac{1}{2}\sqrt{\frac{1}{2}-\frac{{\left(\frac{2}{3}\right)}^{1/3}\left(4+b\right)}{{\left(1\right)}^{1/3}}-\frac{{\left(1\right)}^{1/3}}{2^{1}{3}^{1}}-\frac{1-8b}{4\sqrt{\frac{1}{4}+\frac{11}{{1}^{1}}+\frac{{\left(1\right)}^{1/3}}{2^{111}1}}}},3\right\}$

In the next command, we produce a list of values (not of rules, because we have taken x and applied every rule in bsols to it... These values are the imaginary parts of the solutions x that make the polynomial vanish (and a function of b, because it hasn't been specified yet)

$\mathrm{imb}=\mathrm{ComplexExpand}\left[\mathrm{Im}\left[x/.\mathrm{bsols}\right]\right];$

$\left\{4\right\}$

$-\frac{1}{2}{1}^{1}\mathrm{Sin}\left[\frac{1}{2}\mathrm{Arg}\left[\frac{1}{4}+\frac{1}{1}+\frac{{1}^{1}}{2^{1}1}\right]\right]-1$

And likewise for the real parts of x that solve the polynomial equation

$\mathrm{imr}=\mathrm{ComplexExpand}\left[\mathrm{Re}\left[x/.\mathrm{bsols}\right]\right];$

Plot[] expects a list of functions to plot, The "Flatten" function ensures that Plot is getting a list, but it is redundant in this particular case.  This plot works as follows, for each member in the list, plot the result of replacing b with q for values of q between -10, 10---it is a long-handed way of seeing exactly what is going on and demonstrates the replacement technique.

So the following should be  a plot of the imaginary values of x as a function of b.

$\mathrm{Plot}\left[\mathrm{Evaluate}\left[\mathrm{Flatten}\left[\mathrm{imb}\right]/.b\to q\right],\left\{q,-10,10\right\}\right]$

$⁃\mathrm{Graphics}⁃$

In fact, we should be able to do the  same thing without replacement as the following shows, it is probably instructive to show both ways.

$\mathrm{Plot}\left[\mathrm{Evaluate}\left[\mathrm{imb}\right],\left\{b,-10,10\right\}\right]$

$⁃\mathrm{Graphics}⁃$

There are a few problems that make it difficult to interpret the graph---one is the numerical noise that makes the solutions
jump back and forth; second, because all the colors are the same,  it is not clear which values of x belong to the same solution.  

Let's first try to make each member of the list (remember, there are 4 because it is a fourth-order polynomial and because Dimensions[imb] told us so...

$\mathrm{Plot}\left[\mathrm{Evaluate}\left[\mathrm{Flatten}\left[\mathrm{imb}\right]/.b\to q\right],\left\{q,-10,10\right\},\mathrm{PlotStyle}\to \mathrm{Table}\left[\left\{\mathrm{Hue}\left[1-a/6\right]\right\},\left\{a,1,4\right\}\right]\right]$

$⁃\mathrm{Graphics}⁃$

The plot above is a little better, it looks like the blue curve comes in from the northeast and then then its imaginary part vanishes at a critical values of q (around -0.5), the cyan curve is probably the minus values of the blue curve... and the same thing for yellow and green.  It is much easier to see the branches of solutions for the real parts below.

$\mathrm{Plot}\left[\mathrm{Evaluate}\left[\mathrm{Flatten}\left[\mathrm{imr}\right]/.b\to q\right],\left\{q,-10,10\right\},\mathrm{PlotStyle}\to \mathrm{Table}\left[\left\{\mathrm{Hue}\left[1-a/6\right]\right\},\left\{a,1,4\right\}\right]\right]$

$⁃\mathrm{Graphics}⁃$

But here, because the lines are the same thickness, we don't know if the cyan and blue curves just "stop." Let's find out by also adjusting their thickness.

$\mathrm{Plot}\left[\mathrm{Evaluate}\left[\mathrm{Flatten}\left[\mathrm{imr}\right]/.b\to q\right],\left\{q,-10,10\right\},\mathrm{PlotStyle}\to \mathrm{Table}\left[\left\{\mathrm{Hue}\left[1-a/6\right],\mathrm{Thickness}\left[0.05-\text{.01}*a\right]\right\},\left\{a,1,4\right\}\right]\right]$

$⁃\mathrm{Graphics}⁃$

It is pretty clear that the parameter b is behaving like a "pitchfork" bifurcation---there is one value of x upto a critical value of b, where x splits into two solutions.  This is a picture of two isolated pictchforks.

Created by Mathematica  (October 3, 2005)