Stress Strain, Principal Axes, and Mohr's Circle
General Stress State in Principal Axes System
This is a general state, we will rotate about the z-axis and compare the result to a general two-dimensional stress state.
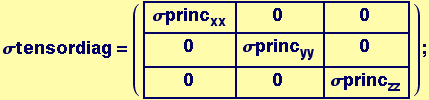
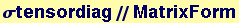
Rotation about z-axis by angle θ
![rotmat[θ_] := ({{Cos[θ], -Sin[θ], 0}, {Sin[θ], Cos[θ], 0}, {0, 0, 1}}) ;](HTMLFiles/Lecture-10_3.gif)
![rotmat[θ]//MatrixForm](HTMLFiles/Lecture-10_4.gif)
Transformation to general two-dimensional stress state coordinate system by rotating the principal system by θ around z-axis
![σrot = Simplify[Transpose[rotmat[θ]] . σtensordiag . rotmat[θ]] ;](HTMLFiles/Lecture-10_5.gif)

Writing the same equation in a slightly different way...
![σrotalt = Collect[σrot//TrigReduce, {Cos[2θ], Sin[2 θ]}] ;](HTMLFiles/Lecture-10_7.gif)

Naming the coefficients of the two-dimensional state in the rotated principal system



Equations 1, 2, and 3 are the equations that express a circle known as Mohr's circle of stress (see accompanying class notes). The equations show the way in which the stress tensor components in a two-dimensional state of stress (a "biaxial" stress state) vary with orientation of the coordinate system in which the stresses are described.
The trace (or twice the offset of Mohr's Circle):
And the determinant
These last two results are precisely the trace and determinant of the x and y terms in the original diagonal form of the stress state, thus illustrating the invariance of these quantities under rotation of coordinate rotations.
Example of Mohr's circle for two-dimensional body in uniaxial tension with = 10 MPa and all other stress components equal to zero
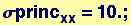


![[Graphics:HTMLFiles/Lecture-10_15.gif]](HTMLFiles/Lecture-10_15.gif)
Comparing this plot with Figure 10-3 in the lecture notes, we see that the maximum and minimum tensile stresses are 10 and 0 MPa (from intercepts with x axis), as expected, and the maximum shear stress is ±5 MPa and it is experienced on a plane oriented at 2θ = 90° or θ = 45° to the tensile axis (remember that angles on Mohr's circle plots are twice the angle in the body).

![]()
![]()
![]()
![]()
![]()
![]()
![[Graphics:HTMLFiles/Lecture-10_15.gif]](HTMLFiles/Lecture-10_15.gif)