Integrals over a Curve, Multidimensional Integrals
We will look at two examples of path integrals of vector functions of position and examine their path dependence. The first integral has a non-zero curl (and so we know that it is not the gradient of some scalar potential)
Here is a vector function (xyz, xyz, xyz) for which the curl does not vanish anywhere
In[1]:=


![CurlVectorFunction = Simplify[Curl[VectorFunction, Cartesian[x, y, z]]]](HTMLFiles/Lecture-14_3.gif)
Out[2]=
Out[3]=
These are the conditions that the curl is zero:
In[45]:=
Out[45]=
There is only one point where this occurs:
In[46]:=
Out[46]=
Let's evaluate the integral of the vector potential ( ∮ •d ) for any curve that wraps around a cylinder of radius R with an axis that coincides with the z-axis
![[Graphics:HTMLFiles/Lecture-14_4.gif]](HTMLFiles/Lecture-14_4.gif)
Any curve that wraps around the cylinder can be parameritized as (x(t), y(t), z(t)) = (R cos(t), R sin(t), A (t)) where (t) = (t + 2π) and in particular (0) = (2π).
Therefore d= (-R sin(t), R cos(t), (t)) dt = (-y(t), x(t), A (t)) dt
The integrand for an integral of "VectorFunction" around such a curve is (written in terms of an arbitrary P(t):
In[4]:=
Out[4]=
The integral depends on the choice of P(t)
In[5]:=
Out[5]=
Let's introduce some specific periodic functions for P. Note how the value of the integral changes as the path changes:
In[6]:=
Out[6]=
In[7]:=
Out[7]=
In[8]:=
Out[8]=
However, here is curious result which shows that some special paths can ``accidentally'' have zero integrals : let P(t) = cos(n t),
In[9]:=
Out[9]=
In[10]:=
Out[10]=
In[14]:=
![[Graphics:HTMLFiles/Lecture-14_5.gif]](HTMLFiles/Lecture-14_5.gif)
Out[14]=
In[24]:=
![[Graphics:HTMLFiles/Lecture-14_6.gif]](HTMLFiles/Lecture-14_6.gif)
Out[24]=
Apparently, the symmetry of the vector function causes cancelation (note results for P = Sin and P=Cos, differ by a minus sign)
But, why doesn't n=1 give us the correct result above? Note that the denominator goes to zero as n→1
Try the same thing with a conservative (curl free, or exact) Vector Function:
Start with a scalar potential
In[25]:=
Out[25]=
Create another vector function that should have a zero curl
In[26]:=
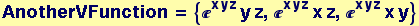
![Simplify[Curl[AnotherVFunction, Cartesian[x, y, z]]]](HTMLFiles/Lecture-14_8.gif)
Out[26]=
Out[27]=
In[28]:=
Out[28]=
The integral depends doesn't on the choice of P(t)
In[29]:=
Out[29]=
In[30]:=
Out[30]=
For a last example, suppose the curl vanishes on the cylindrical surface defined above:
![[Graphics:HTMLFiles/Lecture-14_9.gif]](HTMLFiles/Lecture-14_9.gif)
Suppose we can find a function that has a non-vanishing curl on this surface
In[79]:=
Out[79]=
In[80]:=
Out[80]=
It is easy to see that this is the curl of Stooge, where
In[81]:=
Out[81]=
In fact, we could add to Stooge, any vector function that has vanishing curl--there are an infinite number of these
In[82]:=
Out[82]=
Its integral doesn't care which path around the cylinder it takes, the integrand doesn't depend on P(t)
In[83]:=
Out[83]=
In[84]:=
Out[84]=
Multidimensional Integral over Irregular Domains
We will attempt to model the energy of ion just above one half of a triangular capacitor. Suppose there is a uniformly charged surface (σ≡charge/area=1) occupying an equilaterial triangle in the z=0 plane:
![[Graphics:HTMLFiles/Lecture-14_10.gif]](HTMLFiles/Lecture-14_10.gif)
what is the energy (voltage) of a unit positive charge located at (x,y,z)
The electrical potential goes like , therefore the potential of a unit charge located at (x,y,z) from a small surface patch at (ξ,η,0) is =
Therefore it remains to integrate this function over the domain η∈(0,) and ξ∈ (- ) , (-))
dξdη
Mathematica integrates over the last iterator first:
We will try to find the potential due to a triangular patch on a particle located at (x,y,z=1)
In[31]:=
Out[31]=
Trying to do this directly either takes too long or there is no closed form! We have to work around it by using Indefinite Integrals
In[96]:=
In[97]:=
Out[97]=
In[90]:=
![[Graphics:HTMLFiles/Lecture-14_20.gif]](HTMLFiles/Lecture-14_20.gif)
Out[90]=
In[92]:=
![[Graphics:HTMLFiles/Lecture-14_41.gif]](HTMLFiles/Lecture-14_41.gif)
Out[92]=
The plot above is for a relatively small height z = 1/20 so the contours reveal the triangular shape of the plate at z = 0.
Now look at a somewhat larger value of z = 1/2. The plot below shows contours that are very nearly circular, indicating that the plate is behaving approximately like an equivalent point charge;
![[Graphics:HTMLFiles/Lecture-14_4.gif]](HTMLFiles/Lecture-14_4.gif)
![[Graphics:HTMLFiles/Lecture-14_5.gif]](HTMLFiles/Lecture-14_5.gif)
![[Graphics:HTMLFiles/Lecture-14_6.gif]](HTMLFiles/Lecture-14_6.gif)
![[Graphics:HTMLFiles/Lecture-14_9.gif]](HTMLFiles/Lecture-14_9.gif)
![[Graphics:HTMLFiles/Lecture-14_10.gif]](HTMLFiles/Lecture-14_10.gif)
![[Graphics:HTMLFiles/Lecture-14_20.gif]](HTMLFiles/Lecture-14_20.gif)