Differential Operators and Harmonic Oscillators

Operator Calculus to Solve Heterogeneous Second-Order Linear ODEs

Does Mathematica  apply the Fourier Transform/Derivative Rule Automagically?

$\mathrm{FourierTransform}\left[D\left[f\left[x\right],\left\{x,1\right\}\right],x,k\right]$

$-ik\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]$

It does as of version 5.0! .

$\mathrm{Table}\left[\mathrm{FourierTransform}\left[D\left[f\left[x\right],\left\{x,i\right\}\right],x,k\right],\left\{i,24\right\}\right]//\mathrm{MatrixForm}$

$\left(\text{⁠}\begin{array}{l}-ik\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ -k^2\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ i{k}^3\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ k^4\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ -i{k}^5\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ -k^6\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ i{k}^7\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ k^8\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ -i{k}^9\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ -k^{10}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ i{k}^{11}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ k^{12}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ -i{k}^{13}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ -k^{14}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ i{k}^{15}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ k^{16}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ -i{k}^{17}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ -k^{18}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ i{k}^{19}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ k^{20}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ -i{k}^{21}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ -k^{22}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ i{k}^{23}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\\ k^{24}\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]\end{array}\text{⁠}\right)$

Does  Mathematica apply the rules according to the Fourier Transform being a linear operator?

$\mathrm{FourierTransform}\left[af\left[x\right]+bg\left[x\right],x,k\right]$

$\mathrm{FourierTransform}\left[af\left[x\right]+bg\left[x\right],x,k\right]$

Apparently not--so we make some rules that can be applied. It may be instructive to see how to do this.

$\mathrm{FourierTransform}\left[\text{a\_}\text{f\_}\left[\text{y\_}\right],\text{x\_},\text{k\_}\right]⧴a\mathrm{FourierTransform}\left[f\left[y\right],x,k\right]$

$\mathrm{FourierTransform}\left[\text{expr\_},\text{x\_},\text{k\_}\right]⧴\mathrm{Distribute}\left[\mathrm{FourierTransform}\left[\mathrm{expr},x,k\right],\mathrm{Plus}\right]$

Try them out:

$\mathrm{temp}=\mathrm{FourierTransform}\left[af\left[x\right]+bg\left[x\right]+dp\left[x\right],x,k\right]/.\mathrm{DistributeRule}/.\mathrm{ConstantRule}$

$a\mathrm{FourierTransform}\left[f\left[x\right],x,k\right]+b\mathrm{FourierTransform}\left[g\left[x\right],x,k\right]+d\mathrm{FourierTransform}\left[p\left[x\right],x,k\right]$

Let's  Fourier Transform the left-hand -side of a second-order ODE:

$\mathrm{ODE2nd}=\mathrm{Mass}D\left[y\left[t\right],\left\{t,2\right\}\right]+\mathrm{Viscosity}D\left[y\left[t\right],t\right]+\mathrm{SpringK}y\left[t\right]$

$\mathrm{SpringK}y\left[t\right]+\mathrm{Viscosity}{y}^{\prime }\left[t\right]+\mathrm{Mass}{y}^{\mathrm{\prime \prime }}\left[t\right]$

$\mathrm{FrrODE2nd}=\mathrm{FourierTransform}\left[\mathrm{ODE2nd},t,\omega \right]/.\mathrm{DistributeRule}/.\mathrm{ConstantRule}$

$\mathrm{SpringK}\mathrm{FourierTransform}\left[y\left[t\right],t,\omega \right]-i\mathrm{Viscosity}\omega \mathrm{FourierTransform}\left[y\left[t\right],t,\omega \right]-\mathrm{Mass}{\omega }^2\mathrm{FourierTransform}\left[y\left[t\right],t,\omega \right]$

$\mathrm{rhs}=\mathrm{FourierTransform}\left[\mathrm{Cos}\left[\mathrm{\omega 0}t\right],t,\omega \right]$

$\sqrt{\frac{\pi }{2}}\mathrm{DiracDelta}\left[\omega -\mathrm{\omega 0}\right]+\sqrt{\frac{\pi }{2}}\mathrm{DiracDelta}\left[\omega +\mathrm{\omega 0}\right]$

$\mathrm{ftsol}=\mathrm{Solve}\left[\mathrm{FrrODE2nd}⩵\mathrm{rhs},\mathrm{FourierTransform}\left[y\left[t\right],t,\omega \right]\right]$

$\left\{\left\{\mathrm{FourierTransform}\left[y\left[t\right],t,\omega \right]\to \frac{\sqrt{2\pi }\mathrm{DiracDelta}\left[\omega -\mathrm{\omega 0}\right]+\sqrt{2\pi }\mathrm{DiracDelta}\left[\omega +\mathrm{\omega 0}\right]}{2\left(\mathrm{SpringK}-i\mathrm{Viscosity}\omega -\mathrm{Mass}{\omega }^2\right)}\right\}\right\}$

$\mathrm{InverseFourierTransform}\left[\mathrm{FourierTransform}\left[y\left[t\right],t,\omega \right]/.\mathrm{Flatten}\left[\mathrm{ftsol}\right],\omega ,t,\mathrm{Assumptions}\to \mathrm{\omega 0}>0\right]$

$\frac{\left(\mathrm{SpringK}-\mathrm{Mass}{\mathrm{\omega 0}}^2\right)\mathrm{Cos}\left[t\mathrm{\omega 0}\right]+\mathrm{Viscosity}\mathrm{\omega 0}\mathrm{Sin}\left[t\mathrm{\omega 0}\right]}{{\mathrm{SpringK}}^2-2\mathrm{Mass}\mathrm{SpringK}{\mathrm{\omega 0}}^2+{\mathrm{Viscosity}}^2{\mathrm{\omega 0}}^2+{\mathrm{Mass}}^2{\mathrm{\omega 0}}^4}$

Otherwise, the complete solution (i.e., the inhomogeneous plus the homogeneous parts) can be calculated by the DSolve function

$\mathrm{FullSimplify}\left[y\left[t\right]/.\mathrm{DSolve}\left[\left\{\mathrm{Mass}D\left[y\left[t\right],\left\{t,2\right\}\right]+\mathrm{Damper}D\left[y\left[t\right],t\right]+\mathrm{SpringK}y\left[t\right]⩵\mathrm{Cos}\left[{\omega }_{o}t\right],y\left[0\right]==1,y\text{'}\left[0\right]==0\right\},y\left[t\right],t\right],\mathrm{Assumptions}->\mathrm{\omega 0}>0\&\&\mathrm{Mass}>0\&\&\mathrm{Damper}>0\&\&\mathrm{SpringK}>0\right]$

$\left\{\left(e^{-\frac{\left(\mathrm{Damper}+\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}\right)t}{2\mathrm{Mass}}}\left(\mathrm{SpringK}\left(\left(-1+\mathrm{SpringK}\right)\left(\mathrm{Damper}\left(-1+e^{\frac{\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}t}{\mathrm{Mass}}}\right)+\left(1+e^{\frac{\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}t}{\mathrm{Mass}}}\right)\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}\right)+2e^{\frac{\left(\mathrm{Damper}+\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}\right)t}{2\mathrm{Mass}}}\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}\mathrm{Cos}\left[t{\omega }_o\right]\right)+2\mathrm{Damper}{e}^{\frac{\left(\mathrm{Damper}+\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}\right)t}{2\mathrm{Mass}}}\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}\mathrm{Sin}\left[t{\omega }_o\right]{\omega }_o+\left({\mathrm{Damper}}^3\left(-1+e^{\frac{\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}t}{\mathrm{Mass}}}\right)-\mathrm{Damper}\left(-1+e^{\frac{\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}t}{\mathrm{Mass}}}\right)\mathrm{Mass}\left(1+2\mathrm{SpringK}\right)+{\mathrm{Damper}}^2\left(1+e^{\frac{\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}t}{\mathrm{Mass}}}\right)\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}-\left(1+e^{\frac{\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}t}{\mathrm{Mass}}}\right)\mathrm{Mass}\left(-1+2\mathrm{SpringK}\right)\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}-2e^{\frac{\left(\mathrm{Damper}+\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}\right)t}{2\mathrm{Mass}}}\mathrm{Mass}\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}\mathrm{Cos}\left[t{\omega }_o\right]\right){\omega }_o^2+{\mathrm{Mass}}^2\left(\mathrm{Damper}\left(-1+e^{\frac{\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}t}{\mathrm{Mass}}}\right)+\left(1+e^{\frac{\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}t}{\mathrm{Mass}}}\right)\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}\right){\omega }_o^4\right)\right)/\left(2\sqrt{{\mathrm{Damper}}^2-4\mathrm{Mass}\mathrm{SpringK}}\left({\mathrm{SpringK}}^2+\left({\mathrm{Damper}}^2-2\mathrm{Mass}\mathrm{SpringK}\right){\omega }_o^2+{\mathrm{Mass}}^2{\omega }_o^4\right)\right)\right\}$

Functionals: An Introduction to Variational Calculus by way of Variation of Parameters

An early application of introductory calculus involves finding extreme values of a function y = y(x): values of the independent variable x are sought that maximize or minimize y(x). In the calculus of variations, a common problem involves finding an unknown function y(x) that minimizes a different function in which y(x) appears inside an integral. Here we pursue an answer to a problem of this type.

The "quickest" path of running up-hill  can be estimated with a model of how fast one runs up hill.  Given a starting point y(x=0) = 0 and an ending point y(x=1) = 1, the question is to find, among all possible choices of path y(x) that connects the end and starting point, which is the one that takes the least time if there is a hill h(x) that has to be "run-up."
A reasonable model is that running speed is proportional to Cos(climbing-angle)--that is the velocity is 1 for running on a flat surface and goes to zero as the climbing-angle goes to $\frac{\pi }{2}$ .

In this case, the time can be represented as an integral of the unknown y(x) (this is worked out in the accompanying lecture notes)
T[y(x)] = ${\int }_{x=0}^{x=1}$$\sqrt{1+{\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)}^2+{\left(\frac{\mathrm{dh}}{\mathrm{dx}}\right)}^2}$ dx
Suppose that the "hill" has the shape h(x) = $x^2$.

Here, the "real" problem of finding the optimal path from the infinite set of all paths connecting y(x=0) = 0 toy(x=1) = 1  will be replaced by looking at all second-order polynomials: y(x) = a + bx + c$x^2$

$\mathrm{General}\text{::}\mathrm{spell1}:\text{Possible spelling error: new symbol name "}\mathrm{YGeneral}\text{" is similar to existing symbol "}\mathrm{General}\text{".}\mathrm{More\dots }$

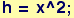
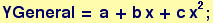
The general path must satisfy the boundary conditions:

$\mathrm{YSatisifyingBCs}=\mathrm{YGeneral}/.\left(\mathrm{Solve}\left[\left\{\left(\mathrm{YGeneral}/.x\to 0\right)⩵0,\left(\mathrm{YGeneral}/.x\to 1\right)⩵1\right\},\left\{a,c\right\}\right]//\mathrm{Flatten}\right)$

$bx+\left(1-b\right)x^2$

There is one remaining free variable, it can be determined by minimizing the integral

$\mathrm{TimeIntegral}=\mathrm{Integrate}\left[\mathrm{Sqrt}\left[1+\left(D\left[\mathrm{YSatisifyingBCs},x\right]\right)^2+\left(D\left[h,x\right]\right)^2\right],x\right]$

$\left(-\frac{\left(-1+b\right)b}{4\left(2-2b+b^2\right)}+\frac{x}{2}\right)\sqrt{1+b^2{\left(1-2x\right)}^2+4b\left(1-2x\right)x+8x^2}+\frac{\left(1-b+b^2\right)\mathrm{Log}\left[2\left(\sqrt{1+b^2{\left(1-2x\right)}^2+4b\left(1-2x\right)x+8x^2}+\frac{b+4x-4bx+b^2\left(-1+2x\right)}{\sqrt{2-2b+b^2}}\right)\right]}{2{\left(2-2b+b^2\right)}^{3/2}}$

$\mathrm{Time}=\mathrm{Simplify}\left[\left(\mathrm{TimeIntegral}/.x\to 1\right)-\left(\mathrm{TimeIntegral}/.x\to 0\right)\right]$

$\mathrm{General}\text{::}\mathrm{spell1}:\text{Possible spelling error: new symbol name "}\mathrm{Time}\text{" is similar to existing symbol "}\mathrm{Times}\text{".}\mathrm{More\dots }$

$\frac{1}{4}\left(\frac{\left(-1+b\right)b\sqrt{1+b^2}}{2-2b+b^2}+\frac{\sqrt{9-4b+b^2}\left(4-3b+b^2\right)}{2-2b+b^2}-\frac{2\left(1-b+b^2\right)\mathrm{Log}\left[2\left(\sqrt{1+b^2}-\frac{\left(-1+b\right)b}{\sqrt{2-2b+b^2}}\right)\right]}{{\left(2-2b+b^2\right)}^{3/2}}+\frac{2\left(1-b+b^2\right)\mathrm{Log}\left[2\left(\sqrt{9-4b+b^2}+\frac{4-3b+b^2}{\sqrt{2-2b+b^2}}\right)\right]}{{\left(2-2b+b^2\right)}^{3/2}}\right)$

$\mathrm{Plot}\left[\mathrm{Time},\left\{b,-2,2\right\}\right]$

$⁃\mathrm{Graphics}⁃$

OK, the time is a minimum somewhere on the interval 0 < b < 1.  Solving for the value of b at the minimum:

$\mathrm{Bminsol}=\mathrm{FindMinimum}\left[\mathrm{Time},\left\{b,0,1\right\}\right]$

$\left\{1.7856694574497398,\left\{b\to 0.5738513944467644\right\}\right\}$

Now we can write the desired fuction that minimizes the time and plot it:

$\mathrm{YCubicSolution}=\mathrm{YSatisifyingBCs}/.\mathrm{Bminsol}\left[\left[2\right]\right]$

$0.5738513944467644x+0.42614860555323564x^2$

$\mathrm{ApproxSolution}=\mathrm{Plot}\left[\mathrm{YCubicSolution},\left\{x,0,1\right\}\right]$

$⁃\mathrm{Graphics}⁃$

The exact minimizing path can be found by using Calculus of Variations. The solution is obtained from a boundary-value problem which we do not take up at this point, but it is interesting to see the exact solution and compare it with the approximate one we obtained above.  The closed-form expression for the function that minimizes the climbing time is:

$\text{}\mathrm{YExactSolution}=\frac{\left(2x\sqrt{1+4x^2}+\mathrm{ArcSinh}\left[2x\right]\right)}{\left(2\sqrt{5}+\mathrm{ArcSinh}\left[2\right]\right)};$

and a series approimation to this function is:

$\mathrm{Series}\left[\mathrm{YExactSolution},\left\{x,0,6\right\}\right]//\mathrm{Normal}//N$

$0.6761586459535304x+0.4507724306356869x^3-0.27046345838141217x^5$

Now plot the exact solution and compare it to our calculated approximation...

$\mathrm{ExactSolution}=\mathrm{Plot}\left[\mathrm{YExactSolution},\left\{x,0,1\right\},\mathrm{PlotStyle}\to \left\{\mathrm{Thickness}\left[0.005\right],\mathrm{Hue}\left[1\right]\right\}\right]$

$\mathrm{General}\text{::}\mathrm{spell1}:\text{Possible spelling error: new symbol name "}\mathrm{ExactSolution}\text{" is similar to existing symbol "}\mathrm{YExactSolution}\text{".}\mathrm{More\dots }$

$⁃\mathrm{Graphics}⁃$

$\mathrm{Show}\left[\mathrm{ApproxSolution},\mathrm{ExactSolution}\right]$

$⁃\mathrm{Graphics}⁃$

These two curves are very close!

Created by Mathematica  (November 23, 2005)