Systems of Differential Equations

A Predator-Prey Model

The traditional "predator-prey" model involves modelling the populations of predators and their prey.  The changes in populations are related: more prey feed more predators, but an overpopulation of predators can lead to depletion of prey, causing a depopulation of predators...  The problem simulated below is a take-off on the traditional one.

This is a model for what fraction of the MIT population would know a particular joke, the joke is told a fraction of the time when a person who has heard it meets someone who hasn't. The rate of joke spreading is proportional to how funny it is.

It is a closely held secret that Susan Hockfield, MIT's president, has an odd sense of humor--she will not let anyone graduate who cannot tell him the joke on graduation day.  This often is a source of embarassment and confusion to the happy families.

Some people who have heard the joke forget it, depending on how forgetful they are:

A certain fraction of new students added to the population each day who presumably don't know the joke, the graduation rate is proportional to the entrance rate and the fraction of those who know the joke.

The fraction of students who remain naive tomorrow is

$\mathrm{TomorrowsNaive}\left[\text{TodaysNaive\_},\text{TodaysJaded\_}\right]:=\mathrm{TodaysNaive}+\frac{\mathrm{FreshmanEntranceRate}}{365}-\frac{\mathrm{JokeSpreadRate}\left[\mathrm{TodaysNaive},\mathrm{TodaysJaded}\right]}{365}$

The fraction of students who will know the joke tomorrow is

$\mathrm{TomorrowsJaded}\left[\text{TodaysNaive\_},\text{TodaysJaded\_}\right]:=\mathrm{TodaysJaded}+\frac{\mathrm{JokeSpreadRate}\left[\mathrm{TodaysNaive},\mathrm{TodaysJaded}\right]}{365}-\frac{\mathrm{ForgotJoke}\left[\mathrm{TodaysNaive},\mathrm{TodaysJaded}\right]}{365}-\frac{\mathrm{GraduationRate}\left[\mathrm{TodaysNaive},\mathrm{TodaysJaded}\right]}{365}$

The population evolves each day as

$\mathrm{TomorrowsPopulation}\left[\left\{\text{TodaysNaive\_},\text{TodaysJaded\_}\right\}\right]:=\left\{\mathrm{TomorrowsNaive}\left[\mathrm{TodaysNaive},\mathrm{TodaysJaded}\right],\mathrm{TomorrowsJaded}\left[\mathrm{TodaysNaive},\mathrm{TodaysJaded}\right]\right\}$

Calculate the population after 5000 days from now if currently 1/5 of the students are naive and 4/5 of the students are in the know.

$\mathrm{NestList}\left[\mathrm{TomorrowsPopulation},\left\{\text{.2},\text{.8}\right\},5000\right]//\mathrm{Short}$

$\left\{\left\{0.2,0.8\right\},4999,\left\{0.6675982286750961,0.580752958296795\right\}\right\}$

Now do a longer calculation with the initial naive fraction 0.24 and the jaded fraction 0.76, and use ListPlot to display the trajectory on the naive–jaded plane. Note how the trajectory spirals in to a specific point in the plane. This is an example of a critical point at which the rates of change of each population become zero.

$\mathrm{ListPlot}\left[\mathrm{NestList}\left[\mathrm{TomorrowsPopulation},\left\{\text{.24},\text{.76}\right\},20000\right],\mathrm{PlotRange}\to \mathrm{All},\mathrm{PlotJoined}\to \mathrm{True},\mathrm{PlotStyle}\to \left\{\mathrm{Hue}\left[\mathrm{Random}\left[\right]\right],\mathrm{Thickness}\left[0.005\right]\right\},\mathrm{AxesLabel}\to \left\{''Naive'',''Jaded''\right\}\right]$

$⁃\mathrm{Graphics}⁃$

Now calculate trajectories for a variety of initial conditions for the jaded and naive populations, selected randomly, then plot them on the naive–jaded plane:

$\mathrm{graphicslist}=\mathrm{Table}\left[\mathrm{ListPlot}\left[\mathrm{NestList}\left[\mathrm{TomorrowsPopulation},\left\{\mathrm{Random}\left[\right],\mathrm{Random}\left[\right]\right\},20000\right],\mathrm{PlotRange}\to \mathrm{All},\mathrm{PlotJoined}\to \mathrm{True},\mathrm{PlotStyle}\to \left\{\mathrm{Hue}\left[\mathrm{Random}\left[\right]\right],\mathrm{Thickness}\left[0.005\right]\right\},\mathrm{DisplayFunction}\to \mathrm{Identity}\right],\left\{i,1,10\right\}\right]$

$\left\{⁃\mathrm{Graphics}⁃,⁃\mathrm{Graphics}⁃,⁃\mathrm{Graphics}⁃,⁃\mathrm{Graphics}⁃,⁃\mathrm{Graphics}⁃,⁃\mathrm{Graphics}⁃,⁃\mathrm{Graphics}⁃,⁃\mathrm{Graphics}⁃,⁃\mathrm{Graphics}⁃,⁃\mathrm{Graphics}⁃\right\}$

$\mathrm{Show}\left[\mathrm{graphicslist},\mathrm{DisplayFunction}\to \mathrm{\$DisplayFunction},\mathrm{AxesLabel}\to \left\{''Naive'',''Jaded''\right\}\right]$

$⁃\mathrm{Graphics}⁃$

Note that all starting points produce trajectories that converge on the same critical point. This is an example of a system of equations that exhibits a stable critical point.
Note also that some of the trajectories take the system into unphysical states where one of the populations exceeds a fraction of 1!

Analysis of Stability of the Predator-Prey Model

The model above can be written as the system of ODEs:
$\frac{\mathrm{dN}}{\mathrm{dt}}$ = α - ρ N J
$\frac{\mathrm{dJ}}{\mathrm{dt}}$ = -αJ  +  ρ N J  - φJ

Find the fixed points:

$\mathrm{General}\text{::}\mathrm{spell1}:\text{Possible spelling error: new symbol name "}\mathrm{Ndot}\text{" is similar to existing symbol "}\mathrm{Not}\text{".}\mathrm{More\dots }$

$\alpha -JN\rho$

$\mathrm{General}\text{::}\mathrm{spell1}:\text{Possible spelling error: new symbol name "}\mathrm{Jdot}\text{" is similar to existing symbol "}\mathrm{Ndot}\text{".}\mathrm{More\dots }$

$-J\alpha +JN\rho -J\varphi$

$\mathrm{fixedpoint}=\mathrm{Solve}\left[\left\{\mathrm{Ndot}⩵0,\mathrm{Jdot}⩵0\right\},\left\{N,J\right\}\right]//\mathrm{Flatten}$

$\left\{J\to \frac{\alpha }{\alpha +\varphi },N\to \frac{\alpha +\varphi }{\rho }\right\}$

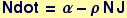
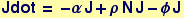
The next final part of this notebook examines the stability of the critical point for this problem. This is discussed in Kreyszig AEM, pp. 170–174.  Kreyszig describes the stability analysis in terms of an eigenvalue problem. The matrix for which eigenvalues are calculated is the "Jacobian" defined below. It is the same as the matrix A in Kreyszig's Eq. (1) on p. 170.

Define the general Jacobian

$\left(\begin{array}{ll}-J\rho & -N\rho \\ J\rho & -\alpha +N\rho -\varphi \end{array}\right)$

Find the Jacobian at the fixed point:

$\left(\begin{array}{ll}-\frac{\alpha \rho }{\alpha +\varphi }& -\alpha -\varphi \\ \frac{\alpha \rho }{\alpha +\varphi }& 0\end{array}\right)$

Approach 1: Compute parameters p, q, and Δ defined in Kreyszig's Eq. (7) on p. 171:

$\mathrm{Kreyszigp}=\mathrm{JacobFixedPoint}\left[\left[1,1\right]\right]+\mathrm{JacobFixedPoint}\left[\left[2,2\right]\right]$

$-\frac{\alpha \rho }{\alpha +\varphi }$

$\mathrm{pValue}=\mathrm{Kreyszigp}/.\left\{\alpha \to \mathrm{FreshmanEntranceRate},\rho \to \mathrm{JokeFunniness},\varphi \to \mathrm{PopulationForgetfullness}\right\}$

$\mathrm{General}\text{::}\mathrm{spell1}:\text{Possible spelling error: new symbol name "}\mathrm{pValue}\text{" is similar to existing symbol "}\mathrm{Value}\text{".}\mathrm{More\dots }$

$-0.36000000000000004$

$\mathrm{Kreyszigq}=\mathrm{Simplify}\left[\mathrm{Det}\left[\mathrm{JacobFixedPoint}\right]\right]$

$\mathrm{General}\text{::}\mathrm{spell1}:\text{Possible spelling error: new symbol name "}\mathrm{Kreyszigq}\text{" is similar to existing symbol "}\mathrm{Kreyszigp}\text{".}\mathrm{More\dots }$

$\alpha \rho$

$\mathrm{qValue}=\mathrm{Kreyszigq}/.\left\{\alpha \to \mathrm{FreshmanEntranceRate},\rho \to \mathrm{JokeFunniness},\varphi \to \mathrm{PopulationForgetfullness}\right\}$

$\mathrm{General}\text{::}\mathrm{spell}:\text{Possible spelling error: new symbol name "}\mathrm{qValue}\text{" is similar to existing symbols}\left\{\mathrm{pValue},\mathrm{Value}\right\}\text{.}\mathrm{More\dots }$

$0.1584$

$\mathrm{DeltaValue}={\mathrm{pValue}}^2-4\mathrm{qValue}$

$-0.504$

According to Kreyszig's Eq. (9) on p. 172, when p ≠ 0 and Δ < 0, the critical point will be a spiral point. In addition, according to Kreyszig's Eq. (10) on p. 173, when p ≤ 0 and q > 0, the critical point will be stable. These findings correspond to what we observed on the trajectories plotted above.

Approach 2: Compute eigenvalues of the Jacobian at the fixed point and use them in a way not described in Kreyszig...

$\mathrm{evals}=\mathrm{Eigenvalues}\left[\mathrm{JacobFixedPoint}\right]$

$\left\{\frac{-\alpha \rho -\sqrt{{\alpha }^2{\rho }^2-4\left(\alpha +\varphi \right)\left({\alpha }^2\rho +\alpha \rho \varphi \right)}}{2\left(\alpha +\varphi \right)},\frac{-\alpha \rho +\sqrt{{\alpha }^2{\rho }^2-4\left(\alpha +\varphi \right)\left({\alpha }^2\rho +\alpha \rho \varphi \right)}}{2\left(\alpha +\varphi \right)}\right\}$

The Eigenvalues will always have a negative real part because the input parameters are positive real coefficients

Considering the parameters used above, the solution is attracted to the fixed point but oscillates

$\mathrm{MitEvals}=\mathrm{evals}/.\left\{\alpha \to \mathrm{FreshmanEntranceRate},\rho \to \mathrm{JokeFunniness},\varphi \to \mathrm{PopulationForgetfullness}\right\}$

$\left\{-0.18000000000000002-0.354964786985977i,-0.18000000000000002+0.354964786985977i\right\}$

The Oscillation perioid is about 18 years

$2\pi /\mathrm{Im}\left[\mathrm{MitEvals}\left[\left[1\right]\right]\right]$

$-17.700869318701763$

Created by Mathematica  (November 21, 2005)