Problem Set 3: Expressivo

To get started, download the assignment code and initialize a repository. If you need a refresher on how to create your repository, see Problem Set 0 .

Wouldn’t it be nice not to have to differentiate all our calculus homework by hand every time? Wouldn’t it be just lovely to type it into a computer and have the computer do it for us instead? For example, we could interact with it like this (user input in green ):

> x * x * x
x*x*x

> !simplify x=2
8

> !d/dx
(x*x)*1+(x*1+1*x)*x

> !simplify x=0.5000
.75

> x * y
x*y

> !d/dy
0*y+x*1

In this system, a user can enter either an expression or a command .

An expression is a polynomial consisting of:

• + and * (for addition and multiplication)
• nonnegative numbers in decimal representation, which consist of digits and an optional decimal point (e.g. 7 and 4.2 )
• variables, which are case-sensitive nonempty sequences of letters (e.g. y and Foo )
• parentheses (for grouping)

Order of operations uses the standard PEMDAS rules.

Space characters around symbols are irrelevant and ignored, so 2.3*pi means the same as 2.3 * pi . Spaces may not occur within numbers or variables, so 2 . 3 * p i is not a valid expression.

When the user enters an expression, that expression becomes the current expression and is echoed back to the user (user input in green ):

> x * x * x
x*x*x

> x + x * x * y + x
x + x*x*y + x

A command starts with ! . The command operates on the current expression, and may also update the current expression. Valid commands:

d/d var
produces the derivative of the current expression with respect to the variable var , and updates the current expression to that derivative

simplify var 1 = num 1 ... var n = num n
substitutes num _i for var _i in the current expression, and evaluates it to a single number if the expression contains no other variables; does not update the current expression

Entering an invalid expression or command prints an error but does not update the current expression. The error should include a human-readable message but is not otherwise specified.

More examples:

> x * x * x
x*x*x

> 3xy
ParseError: unknown expression

> !d/dx
(x*x)*1+(x*1+1*x)*x

> !d/dx
(x*x)*0+(x*1+1*x)*1+(x*1+1*x)*1+(x*0+1*1+x*0+1*1)*x

> !d/d
ParseError: missing variable in derivative command

> !simplify
(x*x)*0+(x*1+1*x)*1+(x*1+1*x)*1+(x*0+1*1+x*0+1*1)*x

> !simplify x=1
6.0

> !simplify x=0 y=5
0

The three things that a user can do at the console correspond to three provided method specifications in the code for this problem set:

• Expression.parse()
• Commands.differentiate()
• Commands.simplify()

These methods are used by Main to provide the console user interface described above.

Problem 1: we will create the Expression data type to represent expressions in the program.

Problem 2: we will create the parser that turns a string into an Expression , and implement Expression.parse() .

Problems 3-4: we will add new Expression operations for differentiation and simplification, and implement Commands.differentiate() and Commands.simplify() .

---

Define an immutable, recursive abstract data type to represent expressions as abstract syntax trees.

Your AST should be defined in the provided Expression interface (in Expression.java ) and implemented by several concrete variants, one for each kind of expression. Each variant should be defined in its own appropriately-named .java file.

Concrete syntax in the input, such as parentheses and whitespace, should not be represented at all in your AST.

1.1 Expression

To repeat, your data type must be immutable and recursive . Follow the recipe for creating an ADT:

• Spec . Choose and specify operations. For this part of the problem set, the only operations Expression needs are creators and producers for building up an expression, plus the standard observers toString() , equals() , and hashCode() . We are strengthening the specs for these standard methods; see below.
• Test . Partition and test your operations in ExpressionTest.java , including tests for toString() , equals() , and hashCode() . Note that we will not run your test cases on other implementations, just on yours.
• Code . Write the rep for your Expression as a data type definition in a comment inside Expression . Implement the variant classes of your data type.

Remember to include a Javadoc comment above every class and every method you write; define abstraction functions and rep invariants, and write checkRep; and document safety from rep exposure.

1.2 toString()

Define the toString() operation on Expression so it can output itself as a string. This string must be a valid expression as defined above. You have the freedom to decide how to format the output with whitespace and parentheses for readability, but the expression must have the same mathematical meaning.

Your toString() implementation must be recursive, and must not use instanceof .

Use the @Override annotation to ensure you are overriding the toString() inherited from Object .

Remember that your tests must obey the spec. If your toString() tests expect a certain formatting of whitespace and parentheses, you must specify this formatting in your spec.

1.3 equals() and hashCode()

Define the equals() and hashCode() operations on your AST to implement structural equality .

Structural equality defines two expressions to be equal if:

1. the expressions contain the same variables, numbers, and operators;
2. those variables, numbers, and operators are in the same order, read left-to-right;
3. and they are grouped in the same way.

For example, the AST for 1 + x is not equal to the AST for x + 1 , but it is equal to the ASTs for 1+x , (1+x) , and (1)+(x) .

For n -ary groupings where n is greater than 2:

• Such expressions must be equal to themselves. For example, the ASTs for 3 + 4 + 5 and (3 + 4 + 5) must be equal.
• However, whether they are equal or not to different groupings with the same mathematical meaning is not specified , and you should choose an appropriate specification and implementation for your AST. For example, you must determine whether the ASTs for (3 + 4) + 5 and 3 + (4 + 5) are equal.

For equality of numbers, you have the freedom to choose a reasonable definition. Integers that can be represented exactly as a double should be considered equal. For example, the ASTs for x + 1 and x + 1.000 must be equal.

Remember: concrete syntax, including parentheses, should not be represented in your AST. Grouping, for example, should be reflected in the AST’s structure.

Be sure that AST instances which are considered equal according to this definition and according to equals() also satisfy observational equality .

Your equals() and hashCode() implementations must be recursive. Only equals() can use instanceof , and hashCode() must not.

Remember to use the @Override annotation.

Commit to Git. Once you’re happy with your solution to this problem, commit to your repo!

---

Now we will create the parser that takes a string and produces an Expression value from it. The entry point for your parser should be Expression.parse() , whose spec is provided in the starting code.

Examples of valid inputs:

3 + 2.4
3 * x + 2.4
3 * (x + 2.4)
((3 + 4) * x * x)
foo + bar+baz
(2*x    )+    (    y*x    )
4 + 3 * x + 2 * x * x + 1 * x * x * (((x)))

Examples of invalid inputs:

3 *
( 3
3 x

Examples of optional inputs:

2 - 3
(3 * x) ^ 2
6.02e23

You may consider these inputs invalid, or you may choose to support additional features (new operators or number representations) in the input. However, your system may not produce an output with a new feature unless that feature appeared in its input . This way, a client who knows about your extensions can trigger them, but clients who don’t know won’t encounter them unexpectedly.

2.1 Write a grammar

Write an ANTLR grammar for polynomial expressions as described in the overview. A starting ANTLR grammar file can be found in src/expressivo/parser/Expression.g4 . This starting grammar recognizes sums of integers, and ignores spaces.

The file Configuration.g4 contains some common boilerplate that is imported into Expression.g4 . You should not edit Configuration.g4 .

See the reading on parser generators for more information about ANTLR, including links to documentation.

2.2 Implement Expression.parse()

Implement Expression.parse() by following the recipe:

• Spec . The spec for this method is given, but you may strengthen it if you want to make it easier to test.
• Test . Write tests for Expression.parse() and put them in ExpressionTest.java . Note that we will not run your tests on any implementations other than yours.
• Code . Implement Expression.parse() so that it calls the parser generated by your ANTLR grammar. The reading on parser generators discusses how to call the parser and construct an abstract syntax tree from it, including code examples.

A general note on precision: you are only required to handle nonnegative decimal numbers in the range of the double type.

2.3 Run the console interface

Now that Expression values can be both parsed from strings with parse() , and converted back to strings with toString() , you can try entering expressions into the console interface.

Run Main . In Eclipse, the Console view will allow you to type expressions and see the result. Try some of the expressions from the top of this handout.

Commit to Git. Once you’re happy with your solution to this problem, commit to your repo!

---

The symbolic differentiation operation takes an expression and a variable, and produces an expression with the derivative of the input with respect to the variable. The result does not need to be simplified.

For example, the following are correct derivatives :

x*x*x with respect to x
3 * x * x

x*x*x with respect to x
x*x + (x + x)*x

x*x*x with respect to x
( ( x*x )*1 )+( ( ( x*1 )+( 1*x ) )*x )+( 0 )

Incorrect derivatives:

y*y*y with respect to y
3*y^2 uses unexpected operator

y*y*y with respect to y
0 d/dx, should be d/dy

To implement your recursive differentiation operation, use these rules:

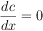
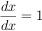
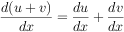
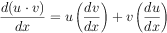
where c is a constant or variable other than the variable we are differentiating with respect to (in this case x ), and u and v can be anything, including x .

3.1. Add an operation to Expression

You should implement differentiation as a method on your Expression datatype, defined recursively. The signature and specification of the method are up to you to design. Follow the recipe:

• Spec . Define your operation in Expression and write a spec.
• Test . Put your tests in ExpressionTest.java . Note that we will not run your test cases on other implementations, just on yours.
• Code . The implementation must be recursive. It must not use instanceof , nor any equivalent operation you have defined that checks the type of a variant.

3.2 Implement Commands.differentiate()

In order to connect your differentiation operation to the user interface, we need to implement the Commands.differentiate() method.

• Spec . The spec for this operation is given, but you may strengthen it if you want to make it easier to test.
• Test . Write tests for differentiate() and put them in CommandsTest.java . These tests will likely be very similar to the tests you used for your lower-level differentiation operation, but they must use Strings instead of Expression objects. Note that we will not run your tests on any implementations other than yours.
• Code . Implement differentiate() . This should be straightforward: simply parsing the expression, calling your differentation operation, and converting it back to a string.

3.3 Run the console interface

We’ve now implemented the !d/d command in the console interface. Run Main and try some derivatives in the Console view.

Commit to Git. Once you’re happy with your solution to this problem, commit to your repo!

---

The simplification operation takes an expression and an environment (a mapping of variables to values). It substitutes the values for those variables into the expression, and attempts to simplfy the substituted polynomial as much as it can.

The set of variables in the environment is allowed to be different than the set of variables actually found in the expression. Any variables in the expression but not the environment remain as variables in the substituted polynomial. Any variables in the environment but not the expression are simply ignored.

The only required simplification is that if the substituted polynomial is a constant expression, with no variables remaining, then simplification must reduce it to a single number, with no operators remaining either. Simplification for substituted polynomials that still contain variables is underdetermined, left to the implementer’s discretion. You may strengthen this spec if you wish to require particular simplifications in other cases.

For example, the following are correct output for simplified expressions:

x*x*x with environment x=5 , y=10 , z=20
125

x*x*x + y*y*y with environment y=10
x*x*x+10*10*10

x*x*x + y*y*y with environment y=10
x*x*x+1000

1+2*3+8*0.5 with empty environment
11.000

Incorrect simplified expressions:

x*x*y with environment x=1 , y=3
1*1*3 not a single number

x*x*x with environment x=2
(8) includes parentheses

x*x*x with empty environment
x^3 uses unexpected operator

Optional simplified expressions:

x*x*y + y*(1+x) with environment x=2
7*y

x*x*x + x*x*x with empty environment
2*x*x*x

4.1 Add an operation to Expression

You should implement simplification as a method on your Expression datatype, defined recursively. The signature and specification of the method are up to you to design. Follow the recipe:

• Spec . Define your operation in Expression and write a spec.
• Test . Put your tests in ExpressionTest.java . Note that we will not run your test cases on other implementations, just on yours.
• Code . The implementation must be recursive (perhaps by calling recursive helper methods). It must not use instanceof , nor any equivalent operation you have defined that checks the type of a variant class.

You may find it useful to add more operations to Expression to help you implement the simplify operation. Spec/test/code them using the same recipe, and make them recursive as well where appropriate. Your helper operations should not simply be a variation on using instanceof to test for a variant class.

4.2 Commands.simplify()

In order to connect your simplify operation to the user interface, we need to implement the Commands.simplify() method.

• Spec . The spec for this operation is given, but you may strengthen it if you want to make it easier to test.
• Test . Write tests for simplify() and put them in CommandsTest.java . These tests will likely be very similar to the tests you used for your lower-level simplify operation, but they should use Strings instead of Expression objects. Note that we will not run your tests on any implementations other than yours.
• Code . Implement simplify() . This should be straightforward: simply parsing the expression, calling your simplify operation, and converting it back to a string.

4.3 Run the console interface

We’ve now implemented the !simplify command in the console interface. Run Main and try using it in the Console view.

Commit to Git. Once you’re happy with your solution to this problem, commit to your repo!

---

• Make sure you have documented specifications , in the form of properly-formatted Javadoc comments, for all your types and operations.

• Make sure you have documented abstraction functions and representation invariants , in the form of a comment near the field declarations, for all your implementations.

  With the rep invariant, also say how the type prevents rep exposure.

  Make sure all types use checkRep() to check the rep invariant and implement toString() with a useful representation of the abstract value.

• Make sure you have satisfied the Object contract for all types. In particular, you will need to specify, test, and implement equals() and hashCode() for all immutable types.

• Use @Override when you override toString() , equals() , and hashCode() , to gain static checking of the correct signature.

  Also use @Override when a class implements an interface method, to remind readers where they can find the spec.

• Make sure you have a thorough, principled test suite for every type. Note that Expression ’s variant classes are considered part of its rep, so a single good test suite for Expression covers the variants too.

---