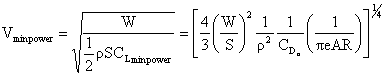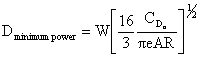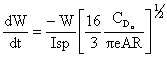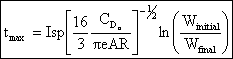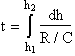IV. Aircraft Performance
In this lecture we will make the connections between aircraft performance and propulsion system performance.
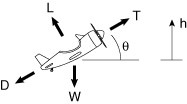
For a vehicle in steady, level flight, the thrust force is equal to the drag force, and lift is equal to weight. Any thrust available in excess of that required to overcome the drag can be applied to accelerate the vehicle (increasing kinetic energy) or to cause the vehicle to climb (increasing potential energy).
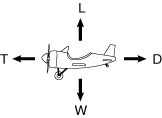
Figure 4.1 Force balance for aircraft in steady level flight.
![]()
Q14 (PDF)
A. Vehicle Drag
Recall from fluids that drag takes the form shown below, being composed of a part termed parasitic drag that increases with the square of the flight velocity, and a part called induced drag, or drag due to lift, that decreases in proportion to the inverse of the flight velocity.
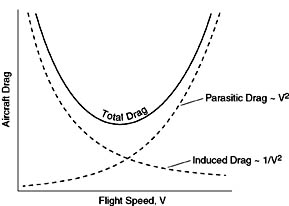
Figure 4.2 Components of vehicle drag.
![]() where
where ![]() and
and ![]()
Thus
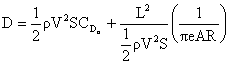 or
or
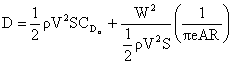
The minimum drag is a condition of interest. We can see that for a given weight, it occurs at the condition of maximum lift-to-drag ratio
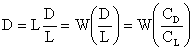
We can find a relationship for the maximum lift-to-drag ratio by setting
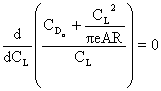
from which we find that
![]() and
and ![]()
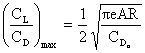 and
and
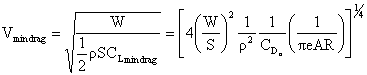
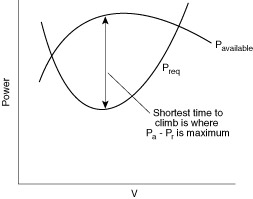
B. Power Required
Now we can look at the propulsion system requirements to maintain steady level flight since
![]()
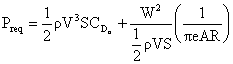
Thus the power required (for steady level flight) takes the form
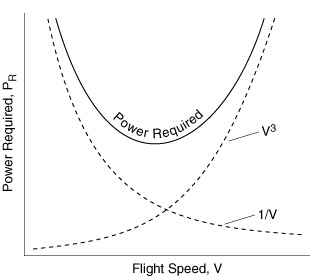
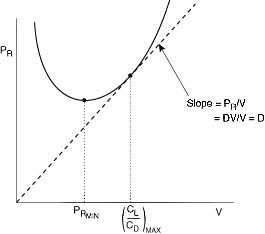
Figure 4.3 Typical power required curve for an aircraft.
The velocity for minimum power is obtained by taking the derivative of the equation for Preq with respect to V and setting it equal to zero.
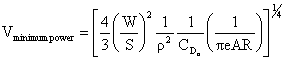
As we will see shortly, maximum endurance (time aloft) occurs when the minimum power is used to maintain steady level flight. Maximum range (distance traveled) is obtained when the aircraft is flown at the most aerodynamically efficient condition (maximum CL/CD).
Homework P4 (PDF)
To see the implications of excess power, visit NASA Glenn - GO! |
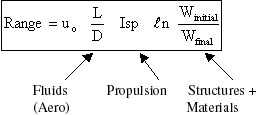
C. Aircraft Range, the Breguet Range Equation
Again, for steady, level flight,
![]()
The weight of the aircraft changes in response to the fuel burned
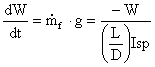
or
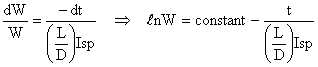
applying the initial conditions, at t = 0 W = Winitial \ const. = ln Winitial
![]()
the time the aircraft has flown corresponds to the amount of fuel burned, therefore
![]()
then multiplying by the flight velocity we arrive at the Breguet Range Equation which applies for situations where Isp and flight velocity are constant over the flight.
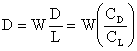 so
so 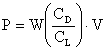
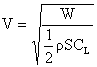
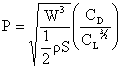
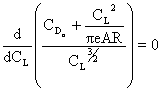
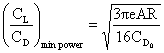 and
and