|
Home | 18.013A | Chapter 26 |
||
|
|
||
You can do even better by providing a rule for estimating the change in y over an interval with the accuracy of Simpson's rule.
To do so we estimate f at the beginning, middle and end of the interval, and give relative weights to these of 1 4 1 as in Simpson's rule. It is only necessary to apply estimates of f at the middle and right endpoints that are accurate "to second order", so that their error is cubic or smaller.
There are many ways to do this. The left hand value for f presents no problems at all and is f(x, y(x)). The Runge-Kutta second order rule involves using
![]()
to approximate the integrand in the middle of the interval, and
![]()
to approximate it at the right end, with
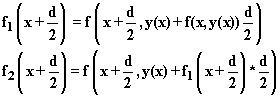
Thus, with the notations given this method provides the following rule
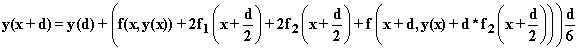
Again, this rule can be implemented without much difficulty on a spreadsheet. You now need a column for each of x, y and the four f terms that occur in this rule, which requires one or two entries and copying for each column. It can be extrapolated as well.
Exercise 26.3 Compute solution to the same equation, y' = y + x using this method with the old initial conditions, y(0) = 1 at x = 1. How much better is it than the previous one for N = 32?
The remarkable thing about this rule is that the error is of fourth order, as it is for Simpson's rule. Thus, if we double the number of intervals the error falls by 16 for large N values. Simpson's rule has the symmetry that makes this so. It is a bit surprising that the estimates here do not have a cubic error term, but they do not have one.
With x in B11 and y in C11 here are the relevant entries for the f 's in D, E, F and G for this equation, to be copied down for the equation y' = y + x
|
f = x + y(x) |
f1 = f + (1 + f)d / 2 |
f + (1 + f1)d / 2 |
f + (1 + f2)d |
|
=B11+C11 |
=D11+(1+D11)*(B12-B11)/2 |
=D11+(1+E11)*(B12-B11)/2 |
=D11+(1+F11)*(B12-B11) |
Here are results for this method at x = 2. The extrapolations start with the assumption that the leading term in the error decreases by a factor of 16 on halving the intervals
|
N\L# |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
11 |
|
exact answer |
= |
11.7781122 |
||
|
2 |
11.670139 |
11.71481481 |
|
||||
|
4 |
11.767941 |
11.77446077 |
11.77638483 |
||||
|
8 |
11.777331 |
11.77795654 |
11.77806931 |
11.77809605 |
|||
|
16 |
11.778058 |
11.7781065 |
11.77811134 |
11.77811201 |
11.77811213 |
||
|
32 |
11.778109 |
11.77811201 |
11.77811218 |
11.7781122 |
11.7781122 |
11.7781122 |
|
|
64 |
11.778112 |
11.77811219 |
11.7781122 |
11.7781122 |
11.7781122 |
11.7781122 |
11.7781122 |
|
Runge-Kutta rule y' = y + x, y(0) = 1, value for y(2) with extrapolations |
|||||||
The proportional errors are indicated here
|
N\L# |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
-0.06606425 |
||||||
|
2 |
-0.00916728 |
-0.00537 |
|||||
|
4 |
-0.0008636 |
-0.00031 |
-0.00015 |
||||
|
8 |
-6.6365E-05 |
-1.3E-05 |
-3.6E-06 |
-1.4E-06 |
|||
|
16 |
-4.6011E-06 |
-4.8E-07 |
-7.3E-08 |
-1.6E-08 |
-5.5E-09 |
||
|
32 |
-3.0291E-07 |
-1.6E-08 |
-1.3E-09 |
-1.6E-10 |
-3.2E-11 |
-1.1E-11 |
|
|
64 |
-1.9431E-08 |
-5.3E-10 |
-2.2E-11 |
-1.4E-12 |
-1.4E-13 |
-1.3E-14 |
8.3E-15 |
|
Runge-Kutta rule y' = y + x, y(0) = 1, proportional error for y(2) with extrapolations |
|||||||
It can be seen that the same number of evaluation points (N for Runge Kutta is comparable to 2N for the trapezoid like rule) yields perhaps a thousand times the accuracy for this evaluation rule in this example, though the best extrapolation for the trapezoid is better than the best unextrapolated Runge-Kutta formula here by a factor of a thousand. See First Order ODE Applet
|
|